Кинематика, динамика и конструирование привода поршневого компрессора, страница 13

Диаграмму аналогов скоростей получают путем дифференцирования графика S(φ). Для этого соединяют ί-1 и ί точку на диаграмме перемещений, параллельным переносом сносят этот отрезок в полюс, продолжают до пересечения с осью О-y, затем ведут из этой точки параллельно оси О-х до пересечения с перпендикуляром к О-х из точки, находящейся между  ί-1 и ί положением. В нулевом и 12 положениях скорость точки Е равна нулю, поэтому график доводят до пересечения с осью О-х. Соединив все эти точки получаем диаграмму аналогов скоростей — S^’(φ).

По диаграмме аналогов скоростей можно определить скорость выходного звена в различных положениях по формуле:

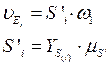                                                                                                 (42)

Пример построения диаграммы аналогов скоростей изображен на рисунке 10.

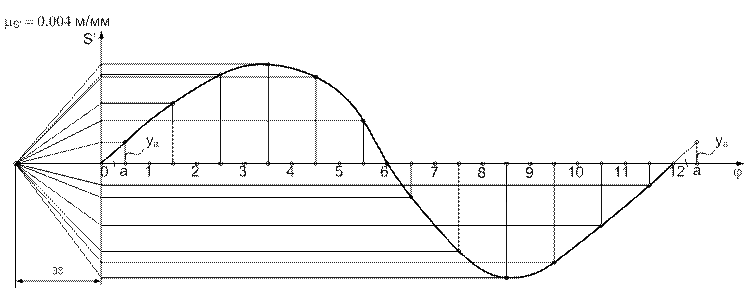
Рисунок 10 - Диаграмма аналогов скоростей

1.6.3 Построение диаграммы аналогов ускорений

Диаграмму аналогов ускорений получают дифференцированием графика S^’(φ). Дифференцирование проводится методом, аналогичным дифференцированию графика S(φ).

После окончания первого цикла (0-12 положение) механизм начинает новый такой же цикл, поэтому мы продолжаем диаграмму аналогов скоростей для завершения диаграммы аналогов ускорений. Для этого мы откладываем от 12 положения по оси абсцисс 10 мм, а по оси О-у расстояние, равное длине перпендикуляра из точки находящейся посередине 0 и 1-ого положения диаграммы аналогов скоростей (Ya на рисунке 10).

Соединив все полученные точки получим диаграмму аналогов ускорений — S’’(φ).

По диаграмме ускорений можно определить ускорение выходного звена в любом положении по формуле:

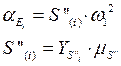                                                                                                  (43)

Например, рассчитаем ускорение точки Е во втором положении:

Пример диаграммы аналогов ускорений изображен на рисунке 11.

Рисунок 11 -  Диаграмма аналогов ускорений

1.7 Анализ результатов по методу планов и диаграмм

Так как метод кинематических диаграмм является приближенным, он используется совместно с методом планов. Между ними существует связь в виде погрешности.

Погрешность для скоростей:

Δ=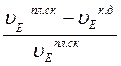·100 %<=5 %.                                                                     (44)

Погрешность для ускорений:

δ=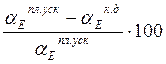 %<=8 %                                                                      (45)

Сделаем проверку для 2,6,9,11 положения.

υ_Е^к.д=у_S’·μ_S’· ω_1.                                                                                         (46)

α_Е^к.д.=у_s’·μ_S’’·ω₁²                                                                                         (47)

Δ₂=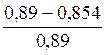·100 % =4 %<5 %;

Δ₆=0 %<5 %;

Δ₉=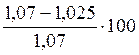 %=4,2%<5 %;

Δ₁₁=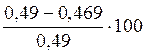 %=4,3%<5 %.

δ ₂=;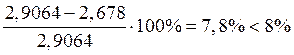

δ₆=;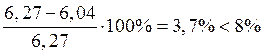

δ₉=;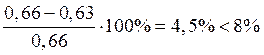

δ₁₁=.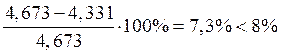

После анализа результатов можем сделать вывод, что значения с планов скоростей и ускорений в сравнении с кинематическими диаграммами находятся в пределах допустимых отклонений.

2 СИЛОВОЙ РАСЧЕТ МЕХАНИЗМОВ

2.1 Основные задачи, цели, методы и принципы силового расчета рычажных механизмов

Основными задачами силового расчета являются:

1)  определение сил, действующих на звенья, а также усилий (реакций), возникающих в кинематических парах при движении механизма;

2)  определение уравновешивающей силы или уравновешивающего момента.

Указанные задачи решаются с целью накопления необходимых данных для последующего прочностного расчета деталей механизмов, выбора рациональных конструктивных форм и размеров звеньев, определения трения в кинематических парах, подбора типов подшипников для кинематических пар, расчета на износ трущихся деталей, подбора сорта и режима смазки, выбора электродвигателя и т.д.

Силовой расчет может быть произведен самыми разнообразными методами. Наибольшее распространение получил метод кинетостатики, использующий обыкновенные уравнения равновесия твердых тел и учитывающий напряду с внешними силами (силами полезных сопротивлений, движущими силами, силами тяжести) силы инерции масс звеньев. Метод кинетостатики основан на принципе Даламбера, который в применении к механизмам может быть сформулирован следующим образом: если ко всем внешним силам, действующим на систему звеньев механизма, добавить силы инерции, то под действием этих сил система звеньев может условно считаться находящейся в равновесии.