8.10. Вычисление двойного интеграла
в декартовых координатах
Если в плоской области ![]() задана
непрерывная функция
задана
непрерывная функция ![]() , то по определению
, то по определению 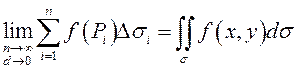 – двойной интеграл от этой функции по области
– двойной интеграл от этой функции по области
![]() (рис.9).
(рис.9).
Выведем правила вычисления двойного интеграла. Сначала рассмотрим область, наиболее просто описываемую в прямоугольной декартовой системе координат.
1. ![]() – координатный прямоугольник.
– координатный прямоугольник.
Пусть
![]() – прямоугольник, ограниченный прямыми
– прямоугольник, ограниченный прямыми ![]() . Так как его стороны параллельны
координатным осям, он называется координатным.
. Так как его стороны параллельны
координатным осям, он называется координатным.
|
По
определению область |
![]() .
.
Применим
двойную нумерацию: ![]() ,
,
![]() (рис.38).
Составим интегральную сумму, соответствующую выбранному разбиению:
(рис.38).
Составим интегральную сумму, соответствующую выбранному разбиению:
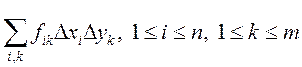 .
.
Такая сумма называется двойной, так как имеет два индекса суммирования, но порядок суммирования пока не определен.
Будем вычислять эту сумму следующим образом: сначала просуммируем по k при фиксированном i, то есть складываем слагаемые, отвечающие одному (любому) столбцу, а затем результаты суммируем по i.
Тогда
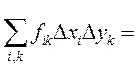
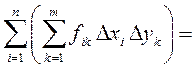
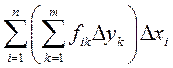 –
такая сумма называется повторной, так как порядок ее вычисления задан.
Конечно, можно суммировать и наоборот: сначала по i, а затем
по k.
–
такая сумма называется повторной, так как порядок ее вычисления задан.
Конечно, можно суммировать и наоборот: сначала по i, а затем
по k.
По
определению определенного интеграла на отрезке при достаточно малом разбиении 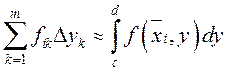 , а
, а 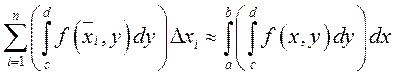 . Переходя
к пределу при
. Переходя
к пределу при ![]() , получим: если
, получим: если ![]() – координатный прямоугольник, то двойной
интеграл
– координатный прямоугольник, то двойной
интеграл
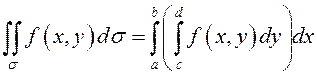 .
.
Интеграл,
стоящий в правой части этого равенства 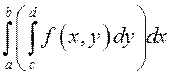 , –
называется повторным. При этом
, –
называется повторным. При этом 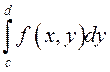 называется
внутренним, а
называется
внутренним, а 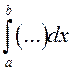 – внешним интегралом. При
вычислении такого повторного интеграла сначала находится внутренний интеграл по
– внешним интегралом. При
вычислении такого повторного интеграла сначала находится внутренний интеграл по
![]() в пределах прямоугольника при фиксированном
значении
в пределах прямоугольника при фиксированном
значении ![]() . Результат его вычисления – функция,
зависящая от
. Результат его вычисления – функция,
зависящая от ![]() . Затем находится внешний интеграл от этой
функции по х в пределах его изменения.
. Затем находится внешний интеграл от этой
функции по х в пределах его изменения.
Другой способ сведения двойной суммы к повторной
приведет нас к такому повторному интегралу: 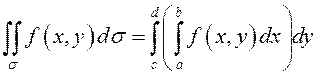 . В
этом случае внутренний интеграл берется по
. В
этом случае внутренний интеграл берется по ![]() при
фиксированном значении
при
фиксированном значении ![]() .
.
Таким образом, чтобы вычислить двойной интеграл, его надо свести к повторному.
ПРИМЕР. Вычислить
двойной интеграл 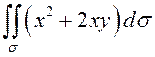 по прямоугольнику
по прямоугольнику ![]() (рис.39).
(рис.39).
|
Запишем повторный интеграл, соответствующий данной области
|
2. ![]() – область вида:
– область вида: ![]() (рис. 40).
(рис. 40).
|
Разобьем область прямыми, параллельными координатным осям, на
достаточно малые части. Фиксируя
Поэтому для того, чтоб лучше представить, каким образом перейти к повторному интегралу в этом случае, проведем вспомогательные линии, пересекающие |
|||||||||||||
область
![]() параллельно оси
параллельно оси ![]() в
направлении возрастания
в
направлении возрастания ![]() (рис.41).
(рис.41).
|
Каждая из таких прямых входит в область на границе Если представить, что отрезок
|
а
так как вспомогательные прямые, пересекающие ![]() параллельно
оси ординат, можно провести от
параллельно
оси ординат, можно провести от ![]() до
до ![]() , то
, то 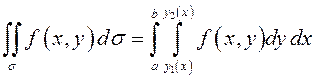 .
.
Итак, чтобы вычислить двойной
интеграл по области такого вида, надо провести вспомогательные прямые,
параллельные оси ![]() , пересекающие область в
направлении возрастания
, пересекающие область в
направлении возрастания ![]() . Переходя к повторному
интегрированию, внутренний интеграл будем вычислять по переменной
. Переходя к повторному
интегрированию, внутренний интеграл будем вычислять по переменной ![]() от линии входа до линии выхода (при
фиксированном
от линии входа до линии выхода (при
фиксированном ![]() ), а внешний – по переменной
), а внешний – по переменной ![]() от
от ![]() до
до ![]() .
.
3. ![]() – область вида:
– область вида: ![]() .
.
|
|
Для такой области проведем вспомогательные прямые, пересекающие
|
ПРИМЕР.
Вычислить 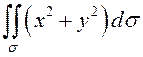 по параллелограмму, ограниченному прямыми
по параллелограмму, ограниченному прямыми ![]() (рис. 43).
(рис. 43).
|
Проведем вспомогательные прямые, параллельные |
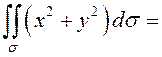
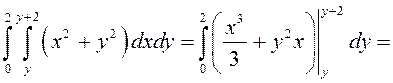
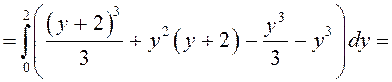
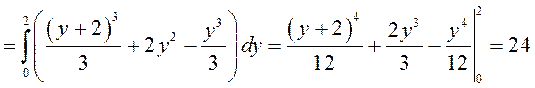 .
.
4. ![]() – произвольная правильная
область.
– произвольная правильная
область.
ОПРЕДЕЛЕНИЕ. Область ![]() называется
правильной в направлении оси
называется
правильной в направлении оси ![]() , если всякая прямая,
параллельная
, если всякая прямая,
параллельная ![]() и проходящая через внутреннюю точку
и проходящая через внутреннюю точку ![]() , пересекает ее границу в двух точках.
Плоская область, правильная в направлениях
, пересекает ее границу в двух точках.
Плоская область, правильная в направлениях ![]() и
и ![]() , называется правильной в декартовых координатах.
, называется правильной в декартовых координатах.
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.