Вычисление двойного интеграла в декартовых координатах. Интеграл Пуассона. Криволинейный и поверхностный интегралы второго рода. Формула Гаусса-Остроградского, страница 7

Теперь расставим пределы интегрирования, учитывая симметрию области относительно плоскости , и вычислим интеграл (рис.67): 

.

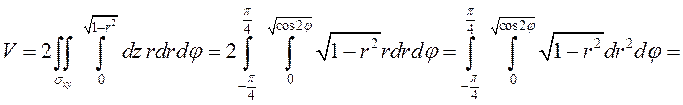
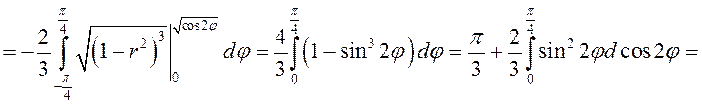
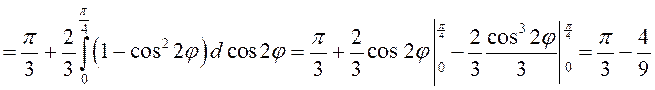2. ВЫЧИСЛЕНИЕ ТРОЙНОГО ИНТЕГРАЛА В СФЕРИЧЕСКОЙ СИСТЕМЕ КООРДИНАТ.

В сферических координатах положение точки  в пространстве определяется тремя числами :  – длина радиус-вектора точки ,  – угол между радиус-вектором  и осью , угол между  ортогональной проекцией  радиус-вектора  и осью , отсчитываемый в положительном направлении (рис. 68).        Для любой точки пространства, очевидно, .

Координатными поверхностями сферической системы координат являются  – сфера с центром в начале координат,  – коническая поверхность с вершиной в начале координат и  – полуплоскость, проходящая через ось  (рис.69).   

Связь между сферическими и декартовыми координатами точек выражается формулами (рис. 68)

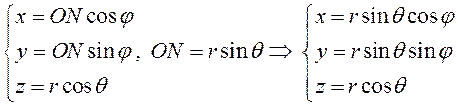                                      (8.20)

Чтобы найти выражение для элемента объёма , разобьем область интегрирования  на малые части  координатными поверхностями и рассмотрим одну такую часть  (рис.70).      

При достаточно мелком разбиении можно считать, что ее объем приблизительно равен объему параллелепипеда с ребрами

. Поэтому  и

                                                                           (8.21)

Тогда, учитывая (8.20), формулу перехода от декартовых координат к сферическим можно записать таким образом:

.

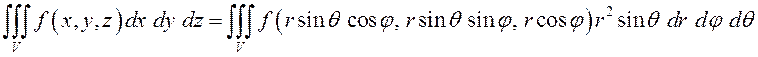При вычислении тройного интеграла в сферических координатах внутренний интеграл всегда берётся по переменной . Наиболее просто выглядят пределы интегрирования, если область  ограничена координатными поверхностями: как и в любой другой системе координат в этом случае пределы интегрирования внутреннего и среднего интегралов будут постоянными.

Это обстоятельство часто является определяющим при выборе соответствующей замены переменных при вычислении тройного интеграла.

ПРИМЕР. Вычислить 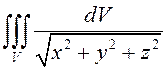, где  ограничена сферой  и конусом 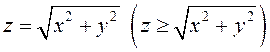  (рис.71).     

Из формул (8.20) следует, что , поэтому . Кроме того, это значит, что внутри .

Чтобы понять, как изменяется угол , заметим, что конус и координатная плоскость пересекаются по линии , которая составляет с осью угол 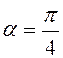, отсюда очевидно, что внутри конуса .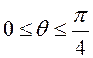

Наконец, из рис.71 ясно, что , следовательно,

.

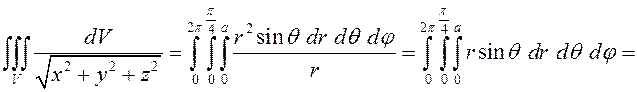
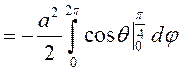
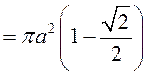8.16. Вычисление криволинейного интеграла первого рода

 (по длине дуги)

1. Пусть плоская кривая  задана явным уравнением

   (рис.72).   

Будем считать, что функция  дифференцируема .    

По определению криволинейный интеграл 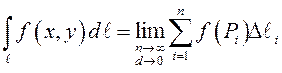, где  – произвольная точка на малом участке дуги , длина которого равна .

Обозначим . Тогда длина малой дуги  вследствие дифференцируемости функции , приблизительно равна длине отрезка , поэтому 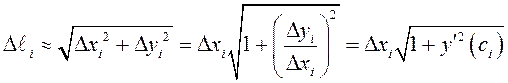 , где  – по теореме Лагранжа (см. гл.5). Переходя к пределу при , получим, что дифференциал дуги  вычисляется по формуле  и 

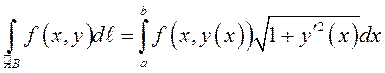                 .                         (8.22)

Таким образом, вычисление  криволинейного интеграла первого рода (его называют криволинейным интегралом по длине дуги) сводится к вычислению определенного интеграла на отрезке.

2. Пусть плоская кривая  задана параметрическими уравнениями:

.

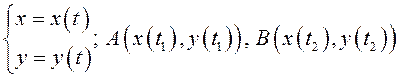Так как производная функции, заданной параметрически, вычисляется по формуле 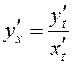 (см. гл.5), то 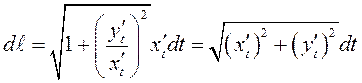. Отсюда получаем формулу для вычисления криволинейного интеграла, в этом случае:

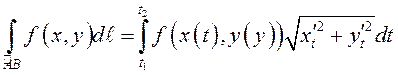     .                     (8.23)

3. Пусть пространственная кривая  задана параметрическими уравнениями: