Вычисление двойного интеграла в декартовых координатах. Интеграл Пуассона. Криволинейный и поверхностный интегралы второго рода. Формула Гаусса-Остроградского, страница 10

ОПРЕДЕЛЕНИЕ. Если криволинейный интеграл 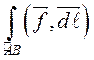 вдоль любого пути, соединяющего точки  и , принимает одно и то же значение, то говорят, что он не зависит от пути интегрирования.

ТЕОРЕМА. Пусть вектор-функция  непрерывна вместе с частными производными 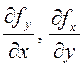 во всех точках правильной области  с кусочно-гладкой границей . Тогда следующие утверждения эквивалентны:

1) для любого кусочно-гладкого контура , лежащего в ,  ;

2) криволинейный интеграл 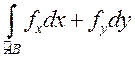 не зависит от пути интегрирования;

3) выражение  является полным дифференциалом некоторой функции, то есть существует функция  такая, что ;

4)  всюду в .

ДОКАЗАТЕЛЬСТВО. Построим доказательство по такой схеме: сначала докажем, что из утверждения 1 следует утверждение 2, затем, что из 2 следует 3, потом покажем, что из 3 следует 4 и, наконец, что из четвертого утверждения следует первое.

1. . 

Пусть  и  – произвольные точки области .      

Соединим их двумя произвольными кусочно-гладкими кривыми  и  (рис.80). Они образовали замкнутый контур  и по условию 1 . Но по свойствам 1 и 2 криволинейного интеграла второго рода

.

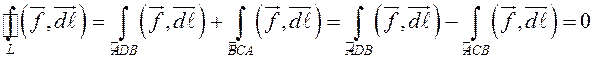Следовательно,

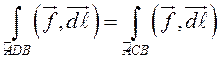, что, ввиду произвольности выбора кривых,  и требовалось доказать.

2. .

Если зафиксировать точку , а  считать произвольной точкой, то значение 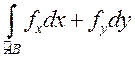 будет зависеть от положения , то есть будет функцией переменных . Обозначим 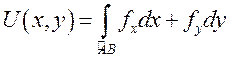. По определению полного дифференциала функции двух переменных 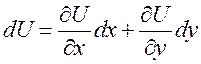 (см. гл. 6). Покажем, что .

По определению частной производной  

.

Так как 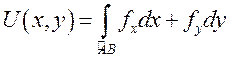 ,  то 

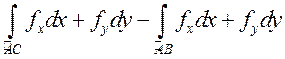, где .

По условию интеграл не зависит от пути интегрирования, поэтому соединим точки  и  отрезком прямой, параллельной оси  (рис.81), и будем считать, что  состоит из   и отрезка . На  , поэтому

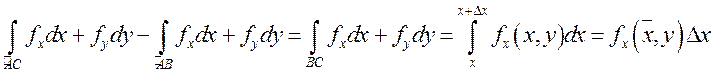, где  находится между  и . Последнее равенство следует из теоремы о среднем значении (8.1).

Таким образом, 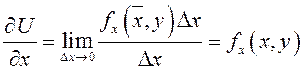, так как  (рис. 81).

Аналогично (рис.82)

.

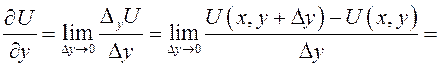
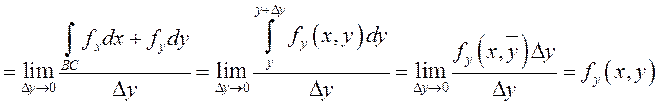Следовательно, .

3. .

Так как 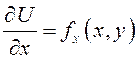, то 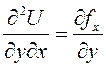;  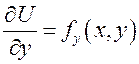 , поэтому . Кроме того, частные производные 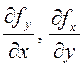 непрерывны по условию теоремы, а, значит, равны, потому что .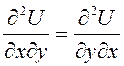

4. .

Пусть  – кусочно-гладкий контур, целиком лежащий в . Тогда по теореме Остроградского-Грина 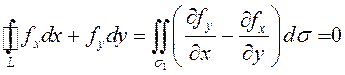 вследствие равенства  всюду в области , ограниченной контуром .

Теорема доказана.

Вернемся к примеру, рассмотренному вначале, и покажем, что интеграл 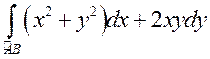   не зависит от пути интегрирования.

.

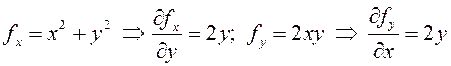Равенство этих производных означает независимость данного криволинейного интеграла от пути интегрирования, поэтому совпадение результатов вычислений  во всех трех рассмотренных случаях было неслучайным.

ЗАМЕЧАНИЕ. Как было отмечено ранее, криволинейный интеграл второго рода можно трактовать как работу переменной силы  по перемещению материальной точки вдоль криволинейного пути . Из доказанной теоремы следует, что выполнение равенства  означает, что сила  консервативна, то есть ее работа зависит от начальной и конечной точек перемещения и не зависит от формы пути.

ЗАМЕЧАНИЕ. Используя доказанную теорему при решении задач, надо внимательно следить за выполнением всех сформулированных в ней условий, иначе можно получить неверный результат.

ПРИМЕР. Вычислить 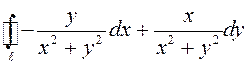, где  – окружность .

Несмотря на то, что 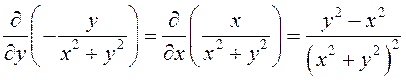     , нельзя сказать, что данный интеграл равен нулю. Дело в том, что вектор-функция  не является непрерывной в начале координат, то есть в центре круга , и доказанная теорема в этом случае не применима.

Чтобы вычислить интеграл, напишем параметрические уравнения окружности  и воспользуемся формулой (9.3):

 .

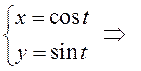
Отметим, что если  – окружность , которая не содержит внутри начало координат, то   .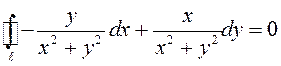

9.5. Поверхностный интеграл второго рода (от вектор-функции)

Рассмотрим задачу о вычислении потока жидкости через заданную поверхность, решение которой приводит к новому понятию поверхностного интеграла второго рода.