ЗАМЕЧАНИЕ. Если поверхность ![]() удобно
проецировать на другую координатную плоскость, то формулы (8.17) и (8.18)
соответствующим образом изменятся.
удобно
проецировать на другую координатную плоскость, то формулы (8.17) и (8.18)
соответствующим образом изменятся.
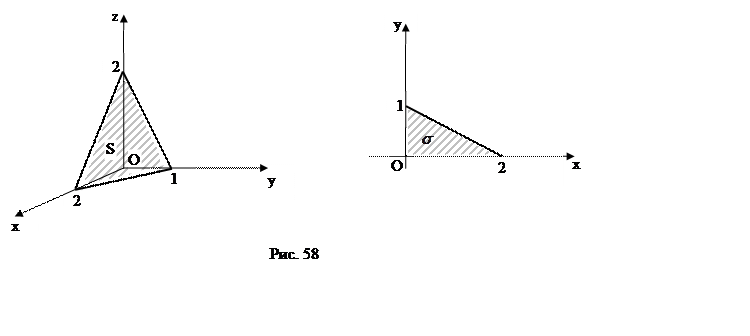 ПРИМЕР.
Вычислить
ПРИМЕР.
Вычислить  , если
, если ![]() часть
плоскости
часть
плоскости ![]() , расположенная в первом октанте (рис.58).
, расположенная в первом октанте (рис.58).
Из уравнения
плоскости получим: ![]()
![]() . Кроме того, во
всех точках плоскости
. Кроме того, во
всех точках плоскости ![]() , поэтому
, поэтому 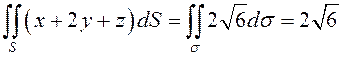 – по свойству 1 определённого интеграла:
площадь проекции
– по свойству 1 определённого интеграла:
площадь проекции ![]() (рис.58), очевидно, равна 1.
(рис.58), очевидно, равна 1.
Рассмотрим немного более сложный пример.
ПРИМЕР. Вычислить  если
если ![]() часть поверхности эллиптического
параболоида
часть поверхности эллиптического
параболоида ![]() , вырезаемая из него цилиндром
, вырезаемая из него цилиндром ![]() (рис.59).
(рис.59).
|
Так как на ![]() и
и ![]() , то, пользуясь (8.17) и (8.18), получим
, то, пользуясь (8.17) и (8.18), получим 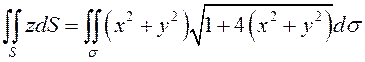 . Проекция
. Проекция ![]() поверхности
поверхности
![]() на плоскость
на плоскость ![]() – круг
(рис.59), поэтому перейдем в двойном интеграле к полярным координатам:
– круг
(рис.59), поэтому перейдем в двойном интеграле к полярным координатам:
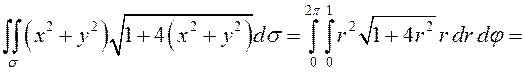 (Замена
(Замена ![]() )
)![]()
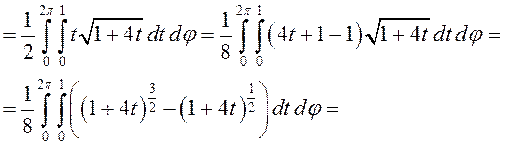
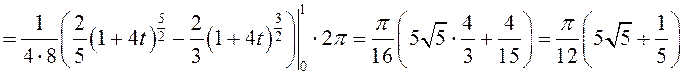 .
.
ЗАМЕЧАНИЕ. Площадь поверхности, задаваемой уравнением ![]() , согласно свойству 1 определенного
интеграла и (8.17) вычисляется по формуле:
, согласно свойству 1 определенного
интеграла и (8.17) вычисляется по формуле:
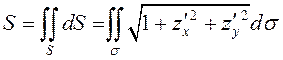 (8.19)
(8.19)
ПРИМЕР. Вычислить площадь части поверхности конуса ![]() , вырезаемой из него цилиндром
, вырезаемой из него цилиндром ![]() (рис.60).
(рис.60).
|
На верхней правой четверти этой
поверхности, где ![]() ,
, ![]()
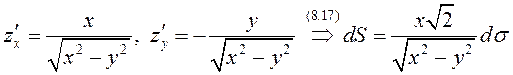 .
.
Отсюда
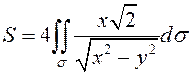 .
.
Так как проекция ![]() этой части
поверхности на плоскость
этой части
поверхности на плоскость ![]() – круговой сектор
– круговой сектор 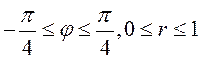 (рис.60), то будем вычислять полученный
двойной интеграл в полярных координатах:
(рис.60), то будем вычислять полученный
двойной интеграл в полярных координатах:
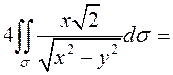
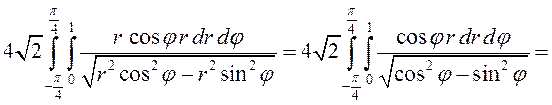
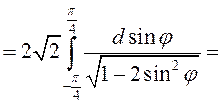
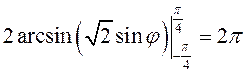 .
.
8.14. Вычисление тройного интеграла
в декартовых координатах
Пусть в пространственной области ![]() задана непрерывная функция
задана непрерывная функция ![]() . По определению тройным интегралом от этой
функции по области
. По определению тройным интегралом от этой
функции по области ![]() называется
называется  , где точки
, где точки ![]()
![]() , а
, а ![]() – малые части области
– малые части области ![]() , на которые она разбивается при
составлении интегральной суммы.
, на которые она разбивается при
составлении интегральной суммы.
Для вычисления тройного интеграла в декартовых
координатах разобьем ![]() на достаточно малые части
плоскостями
на достаточно малые части
плоскостями ![]()
![]() . Тогда
. Тогда ![]() – параллелепипед со сторонами
– параллелепипед со сторонами ![]() , поэтому, очевидно, элемент объема
, поэтому, очевидно, элемент объема ![]() .
.
Заметим, что плоскости ![]() являются
координатными поверхностями декартовой системы координат
являются
координатными поверхностями декартовой системы координат ![]() (аналогично координатным линиям
(аналогично координатным линиям ![]() системы координат
системы координат ![]() ):
на каждой из этих плоскостей изменяются лишь две из трех координат
):
на каждой из этих плоскостей изменяются лишь две из трех координат ![]() .
.
По аналогии с двойным интегралом для того, чтобы вычислить тройной, надо расставить пределы интегрирования, то есть свести тройной интеграл к трехкратному.
Начнем
с самой простой области в системе ![]() .
.
1. ![]() – параллелепипед, грани которого
параллельны координатным плоскостям:
– параллелепипед, грани которого
параллельны координатным плоскостям: ![]() .
.
В
этом случае 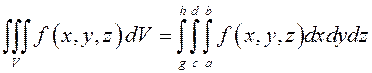 . Внутренний интеграл
. Внутренний интеграл 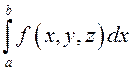 вычисляется по переменной
вычисляется по переменной ![]() при условии, что
при условии, что ![]() .
Результат его вычисления зависит от двух переменных
.
Результат его вычисления зависит от двух переменных ![]() и
и ![]() . Оставшийся после вычисления внутреннего
двойной интеграл вычисляется по проекции параллелепипеда на плоскость
. Оставшийся после вычисления внутреннего
двойной интеграл вычисляется по проекции параллелепипеда на плоскость ![]() .
.
Этот порядок интегрирования не единственный, так как
существует 6 перестановок из трех элементов ![]()
2. ![]() произвольная правильная область.
произвольная правильная область.
Ранее было дано определение правильной области в
системе координат ![]() . Аналогично этому пространственная
область называется правильной, если она правильная в направлениях
осей
. Аналогично этому пространственная
область называется правильной, если она правильная в направлениях
осей ![]() .
.
|
Для того чтобы расставить пределы интегрирования в
тройном интеграле, проведем вспомогательные линии, параллельные оси ![]() и проходящие через внутренние точки
области
и проходящие через внутренние точки
области ![]() (рис.61). Все эти линии попадают в область
(рис.61). Все эти линии попадают в область
![]() на нижней половине поверхности,
ограничивающей область – назовем её поверхностью входа, – а выходят из
области на верхней половине, которая в таком случае является поверхностью
выхода.
на нижней половине поверхности,
ограничивающей область – назовем её поверхностью входа, – а выходят из
области на верхней половине, которая в таком случае является поверхностью
выхода.
Поэтому 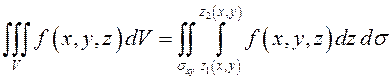 , где
, где ![]() – проекция
– проекция ![]() на
координатную плоскость
на
координатную плоскость ![]() (рис.61). Здесь внутренний
интеграл берется по
(рис.61). Здесь внутренний
интеграл берется по ![]() при фиксированных значениях
при фиксированных значениях ![]() и
и ![]() . После
его вычисления остается найти двойной интеграл по плоской области
. После
его вычисления остается найти двойной интеграл по плоской области ![]() , и окончательный переход от тройного
интеграла к трехкратному может быть, например, таким:
, и окончательный переход от тройного
интеграла к трехкратному может быть, например, таким:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.