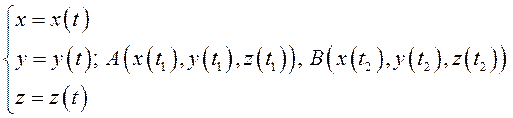Вычисление двойного интеграла в декартовых координатах. Интеграл Пуассона. Криволинейный и поверхностный интегралы второго рода. Формула Гаусса-Остроградского, страница 8

.

Тогда, по аналогии с п. 2, имеем:

.           (8.24)

ЗАМЕЧАНИЕ. Если пространственная кривая задана как результат пресечения двух поверхностей, то ее следует параметризовать, то есть найти способ переписать ее уравнения в параметрическом виде.

ПРИМЕР. Вычислить 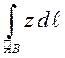 ,  где  – дуга  конической  винтовой линии

.

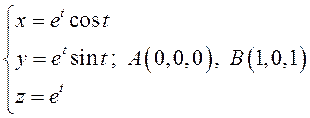Так как , то дифференциал дуги

.

Очевидно, что точке  не соответствует никакое конечное значение параметра , так как , но . Кроме того,  при , поэтому ясно, что точке  соответствует значение параметра . Следовательно,  по формуле (8.24) вычисление данного криволинейного  интеграла  сведётся  к  вычислению  несобственного  интеграла:                                .

ЗАМЕЧАНИЕ. Согласно свойству 1 определенного  интеграла длина дуги вычисляется по формуле 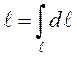. В частности

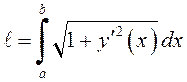                                          (8.25)

– длина дуги плоской кривой, заданной явным уравнением , .

ПРИМЕР. Найти длину дуги кривой .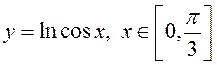

Эта плоская кривая задана явным уравнением,

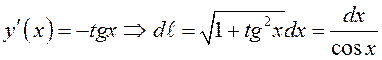  при 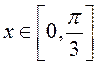. Тогда по формуле (8.25) получим      

.

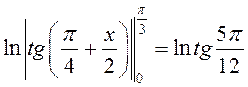Глава 9. КРИВОЛИНЕЙНЫЙ И ПОВЕРХНОСТНЫЙ

ИНТЕГРАЛЫ ВТОРОГО РОДА

9.1. Криволинейный интеграл второго рода (от вектор-функции)

Рассмотрим задачу о вычислении работы переменной силы, решение которой приводит  к  новому понятию  криволинейного  интеграла второго рода.

Пусть под действием переменной по величине и направлению силы  материальная точка перемещается вдоль криволинейного пути  от точки  до точки . Найдем работу этой силы при условии, что кривая  достаточно гладкая, а вектор-функция   непрерывна.

Известно, что если под действием постоянной силы  материальная точка совершает прямолинейное перемещение  (рис. 73), то работа .

В нашем случае сила переменна и путь криволинеен, и потому этой простой формулой мы не сможем воспользоваться сразу. Однако, свести решение поставленной задачи к ее использованию возможно следующим образом.

1) Разобьем  на  достаточно малых частей точками  ( и  совпадают с А и В соответственно) и впишем в кривую  ломаную линию (рис.74). Тогда перемещение вдоль дуги  можно приближенно считать прямолинейным перемещением вдоль вектора , так как кривая  достаточно гладкая по сделанному предположению (рис. 74).

2) Так как, кроме того, вектор-функция  непрерывна, то на малом участке  она изменяется мало, поэтому будем считать, что всюду на таком участке , где  произвольная точка на .

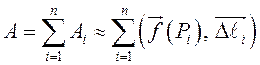3) Обозначим  работу силы   на . Тогда . Если в некоторой декартовой системе координат , а , то  и  – -я интегральная  сумма  для  вектор-функции   на кривой  . Это приближенное значение работы, очевидно, тем точнее, чем больше участков   и меньше их длина.  Поэтому  если существует предел  -й  интегральной суммы, когда  ,    не зависящий от способа ее составления, то за точное значение работы естественно принять его величину:

.

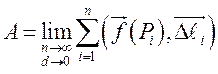Отвлекаясь от физического смысла рассмотренной задачи, можно дать определение новому математическому понятию: если во всех точках гладкой кривой  задана непрерывная вектор-функция , то

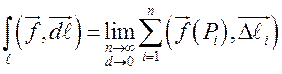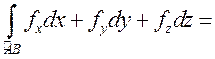
, или  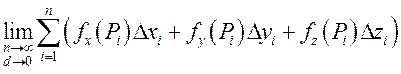 – криволинейный интеграл второго рода (криволинейный интеграл от вектор-функции) при условии, что этот  предел существует и не зависит от способа составления интегральной суммы.

СВОЙСТВА  КРИВОЛИНЕЙНОГО ИНТЕГРАЛА ВТОРОГО РОДА

1. Значение криволинейного интеграла второго рода зависит от направления движения вдоль , именно: .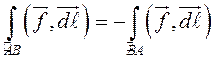

2.   для любых точек А, В, С на кривой – свойство аддитивности.

3. 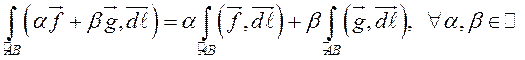 – свойство линейности.

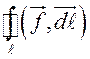ЗАМЕЧАНИЕ. Если криволинейный интеграл второго рода вычисляется по замкнутому контуру, то он называется циркуляцией вектора  вдоль контура  и обозначается . При этом если не оговорено противное, то считается, что направление обхода контура положительно, то есть против часовой стрелки.