Вычисление двойного интеграла в декартовых координатах. Интеграл Пуассона. Криволинейный и поверхностный интегралы второго рода. Формула Гаусса-Остроградского, страница 4

ПРИМЕР. Вычислить площадь области, ограниченной лемнискатой Бернулли  (рис.55).                

ЗАМЕЧАНИЕ. Отметим еще раз, что при вычислении двойного интеграла в декартовых координатах область интегрирования разбивалась на малые части линиями  и , параллельными координатным осям; в полярной системе координат – лучами, исходящими из полюса  и окружностями .  Такие линии называются координатными линиями соответствующей системы координат. Вдоль координатных линий одна из координат изменяется, вторая – остается постоянной.

При вычислении двойного интеграла в любой другой криволинейной системе координат  для нахождения элемента площади  область интегрирования следует разбивать на малые части координатными линиями этой системы координат, то есть кривыми  и .

Вспомогательные линии при переходе к повторному интегралу тоже должны быть координатными линиями, причем внутренний интеграл имеет постоянные пределы интегрирования только тогда, когда  ограничена координатными линиями.

8.12. Интеграл Пуассона

В теории вероятностей большую роль играет несобственный интеграл 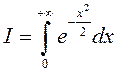, который называется интегралом Пуассона. Как было отмечено в главе 7, функция 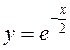 не имеет элементарной первообразной, и неопределенный интеграл 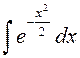 относится к так называемым «неберущимся» интегралам. Однако, вычислить несобственный 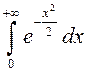 можно. Прежде, чем найти его значение, убедимся в том, что он сходится.  

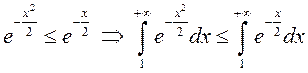Так как , то , но 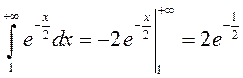, то есть по определению сходимости несобственных интегралов I рода 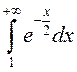 сходится. Поэтому 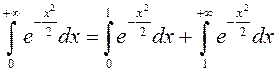  сходится по признаку сравнения.

Для вычисления значения интеграла Пуассона применим такой искусственный прием: рассмотрим двойной интеграл 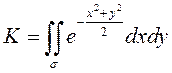, где областью интегрирования является первая четверть координатной плоскости (рис.56).   

В декартовых координатах (вспомним, что величина определенного интеграла не зависит от обозначения переменной интегрирования).

С другой стороны, переходя к полярной системе координат, получим:

       .

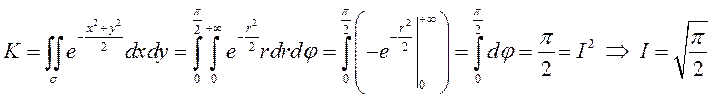Таким образом,                .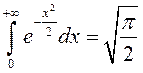

8.13. Вычисление поверхностного интеграла первого рода

(по площади поверхности)

Пусть на поверхности , задаваемой уравнением , определена непрерывная функция  . По определению поверхностным интегралом первого рода от этой функции называется

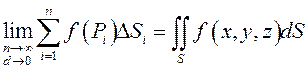, где точки , а  – малые части поверхности , на которые она разбивается при составлении интегральной суммы (рис.10).

Будем считать, что функция  дифференцируема , то есть в любой точке S можно провести касательную плоскость.

Область  является проекцией  на плоскость . Выразим элемент поверхности  через его проекцию  (рис.57). Для этого воспользуемся известным утверждением: если  – проекция плоской области с площадью , то , где угол между плоскостью области и плоскостью проекции.

Проведем в произвольной точке выбранного элемента поверхности  касательную плоскость и пусть  – та её часть, которая проецируется на . Так как функция  дифференцируема, то площадь элемента 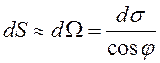 , где  угол между касательной плоскостью и плоскостью , который равен углу между их нормалями.

Вычислим . Если переписать уравнение поверхности  в неявном виде , то  (см. гл. 6), а  поэтому 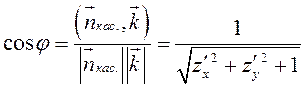    (см. гл. 2).

Следовательно,          

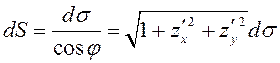                                       .                                (8.17)

В точках поверхности , где , функция  принимает значения , поэтому в соответствии с определением поверхностный интеграл первого рода может быть сведён  к  двойному интегралу:

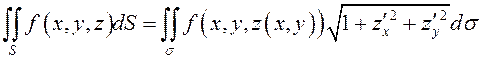.                     (8.18)

Таким образом, вычисление поверхностного интеграла первого рода сводится к вычислению двойного интеграла по проекции данной поверхности на плоскость .