Математика \ Математика

Вычисление двойного интеграла в декартовых координатах. Интеграл Пуассона. Криволинейный и поверхностный интегралы второго рода. Формула Гаусса-Остроградского, страница 13

– здесь при переходе от двойного интеграла к поверхностному учтён знак , использовано равенство (9.9) и свойство аддитивности поверхностного интеграла.

Чтобы доказать равенство 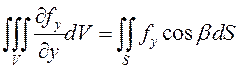, спроецируем область на плоскость (рис.88) , при этом проецирующий цилиндр разобьёт поверхность на две части , .

Как видно из рис. 88 внешняя нормаль к поверхности S образует острый угол с осью на правой части и угол на левой части . Значит на , а на .

Таким образом,

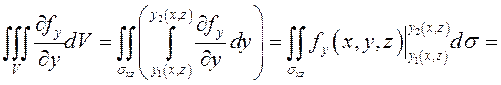
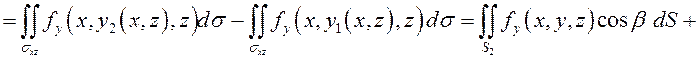
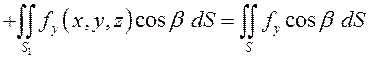Этот результат получен с учетом знака , формулы (9.10) и свойства аддитивности.

Аналогично показывается, что .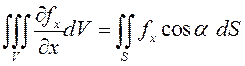

Из полученных равенств очевидным образом следует формула (9.13).

Что и требовалось доказать.

ЗАМЕЧАНИЕ. Можно доказать, что формула Гаусса-Остроградско- го справедлива не только для правильных, но и для любых областей, которые могут быть разбиты цилиндрическими поверхностями на правильные части.

ЗАМЕЧАНИЕ. Выражение 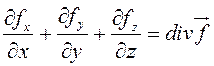называется дивергенцией вектора .

Подчеркнем, что дивергенция – это скалярная характеристика векторной величины.

Поверхностный интеграл второго рода от вектора равен потоку этого вектора через поверхность :

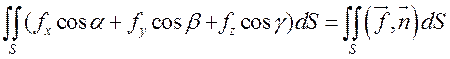, поэтому физический смысл формулы Гаусса-Остроградского состоит в том, что поток вектора через замкнутую поверхность в направлении внешней нормали равен тройному интегралу от дивергенции этого вектора по области, ограниченной этой поверхностью: .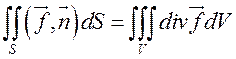

ПРИМЕР. Вычислить поток вектора через поверхность тетраэдра, ограниченного плоскостями

Уравнение плоскости в отрезках имеет вид: 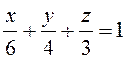. Построим данный тетраэдр (рис.89). Поток вектора через его полную поверхность равен сумме потоков через все грани, и если вычислять его по формуле (9.12), то надо найти шесть двойных интегралов.

Однако тетраэдр представляет собой замкнутую поверхность, поэтому здесь применима формула Гаусса-Остроградского. Найдем дивергенцию вектора :

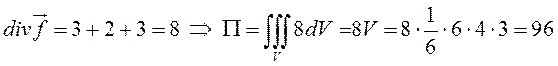, где – объем тетраэдра.

Формулу Гаусса-Остроградского можно применять и к вычислению потока вектора через незамкнутую поверхность. Для этого ее нужно временно замкнуть какой-нибудь вспомогательной поверхностью («крышкой») и, вычислив 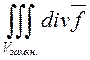, вычесть «лишний» поток через «крышку». Часто это бывает проще, чем непосредственное вычисление потока по формуле (9.12).

Вернемся к ранее рассмотренному примеру в п. 9.5.

ПРИМЕР. Вычислить поток вектора через внешнюю сторону эллиптического параболоида (рис.85).

Замкнём поверхность параболоида вспомогательной поверхностью . Теперь 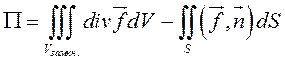, где – круг в плоскости ; значит, – внешняя нормаль к S, . Поэтому при вычислении потока через эту вспомогательную поверхность по формуле (9.12) ненулевым будет только интеграл по проекции . Вычислим и найдем поток: 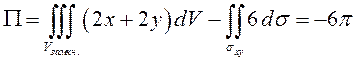, так как тройной интеграл по симметричной относительно осей и области от нечётной функции, очевидно, равен нулю.