Если ![]() не является правильной
областью ни в одном из направлений, то для вычисления двойного интеграла ее
следует разбить на части, правильные в направлении какой-либо из координатных
осей, и воспользоваться свойством аддитивности.
не является правильной
областью ни в одном из направлений, то для вычисления двойного интеграла ее
следует разбить на части, правильные в направлении какой-либо из координатных
осей, и воспользоваться свойством аддитивности.
8.11. Вычисление двойного интеграла
в полярных координатах
Один из способов замены переменных при
вычислении двойного интеграла – переход в полярную систему координат. Делать
такой переход имеет смысл, когда, например, область интегрирования ![]() проще или удобнее описывается в полярных
координатах.
проще или удобнее описывается в полярных
координатах.
Будем считать, что область ![]() – правильная в полярных координатах.
– правильная в полярных координатах.
ОПРЕДЕЛЕНИЕ. Область ![]() называется
правильной в полярных координатах, если всякий луч, исходящий из полюса
и проходящий через её внутреннюю точку, пересекает границу
называется
правильной в полярных координатах, если всякий луч, исходящий из полюса
и проходящий через её внутреннюю точку, пересекает границу ![]() не более чем в двух точках.
не более чем в двух точках.
На рис.49 ![]() – правильная область в
– правильная область в ![]() (но неправильная в
(но неправильная в ![]() );
); ![]() –неправильная
область;
–неправильная
область; ![]() и
и ![]() –
правильные в полярных координатах.
–
правильные в полярных координатах.
|
Чтобы найти выражение для элемента площади ![]() в
полярной системе координат
в
полярной системе координат ![]() , разобьем
, разобьем ![]() на достаточно малые части лучами,
исходящими из полюса, вдоль которых
на достаточно малые части лучами,
исходящими из полюса, вдоль которых ![]() , и концентрическими
окружностями
, и концентрическими
окружностями ![]() . Такие линии называются координатными
линиями полярной системы координат.
. Такие линии называются координатными
линиями полярной системы координат.
Проведем лучи ![]() и
окружности
и
окружности ![]() (рис.50).
(рис.50).
|
Тогда каждую из получившихся таким образом малых частей с площадью
![]() можно приближённо считать прямоугольником со
сторонами
можно приближённо считать прямоугольником со
сторонами ![]() и
и ![]() , где
, где ![]() – длина дуги окружности с центральным
углом
– длина дуги окружности с центральным
углом ![]() радиуса
радиуса ![]() .
Поэтому
.
Поэтому ![]() , а это значит, что, переходя к пределу в
соответствии с определением двойного интеграла, получим:
, а это значит, что, переходя к пределу в
соответствии с определением двойного интеграла, получим:
![]() . (8.15)
. (8.15)
Так как 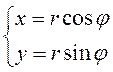 – выражение декартовых координат
точки через полярные, то формула перехода от одной системы координат к другой
имеет вид:
– выражение декартовых координат
точки через полярные, то формула перехода от одной системы координат к другой
имеет вид:
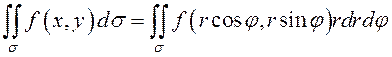 (8.16)
(8.16)
Чтобы вычислить двойной интеграл (8.16), надо перейти к повторному
интегралу, то есть расставить пределы интегрирования в соответствии с заданной
областью ![]() .
.
Пусть граница ![]() области
области
![]() состоит из дуг
состоит из дуг ![]() и
и ![]()
![]() (рис. 51).
(рис. 51).
|
Проведём вспомогательные линии– лучи, исходящие из полюса и
пересекающие
|
ЗАМЕЧАНИЕ. Следует обратить внимание на то, что при
вычислении двойного интеграла в полярных координатах внутренний интеграл
всегда берется по переменной ![]() , а внешний,
соответственно, – по
, а внешний,
соответственно, – по ![]() .
.
Отметим некоторые частные случаи перехода к повторному интегралу в полярной системе координат (рис.52 и 53):
|
|
|
|
ЗАМЕЧАНИЕ. При вычислении двойного интеграла в
полярных координатах внутренний интеграл может иметь постоянные
пределы интегрирования, лишь если ![]() ограничена
координатными линиями, то есть является кругом с центром в полюсе, сектором,
кольцом или его частью. Внешний интеграл всегда имеет постоянные пределы
интегрирования.
ограничена
координатными линиями, то есть является кругом с центром в полюсе, сектором,
кольцом или его частью. Внешний интеграл всегда имеет постоянные пределы
интегрирования.
ПРИМЕР. Вычислить 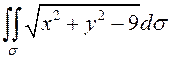 , если
, если ![]() ограничена линиями
ограничена линиями ![]() .
.
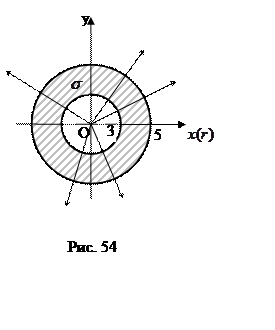
|
Так как область интегрирования является кольцом с центром
в точке |
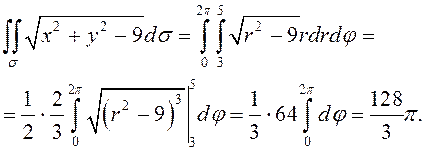
ЗАМЕЧАНИЕ. Площадь плоской области в полярных
координатах согласно
свойству 1 определенного интеграла и (8.15) вычисляется по формуле: 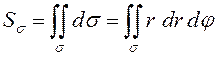 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.