Тогда
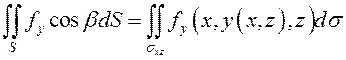 .
(9.10)
.
(9.10)
Если ![]() – тупой угол, то в правой
части этого равенства будет знак «минус».
– тупой угол, то в правой
части этого равенства будет знак «минус».
Наконец, рассуждая аналогично, получим, что
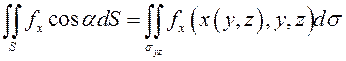 (9.11)
(9.11)
при
условии, что угол 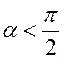 (
(![]() – угол
между осью
– угол
между осью ![]() и нормалью к S).
и нормалью к S).
Таким образом, из равенств (9.9) – (9.11) следует, что
вычисление поверхностного интеграла второго рода можно заменить вычислением
трех двойных интегралов по проекциям ![]() поверхности
поверхности ![]() на координатные плоскости: если
направляющие косинусы нормали к поверхности положительны, то
на координатные плоскости: если
направляющие косинусы нормали к поверхности положительны, то
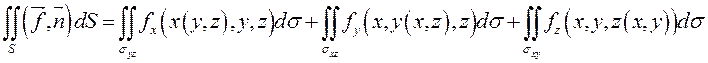 (9.12)
(9.12)
Здесь
![]() – выражения, полученные из уравнения поверхности
– выражения, полученные из уравнения поверхности
![]() разрешением его относительно
соответствующей переменной.
разрешением его относительно
соответствующей переменной.
ЗАМЕЧАНИЕ.
В каждой точке поверхности ![]() можно провести две
единичные нормали: внешнюю и внутреннюю (рис.84).
можно провести две
единичные нормали: внешнюю и внутреннюю (рис.84).
|
Направления этих нормалей противоположны, поэтому если
для внешней нормали, например, ![]() , то для внутренней
нормали будет
, то для внутренней
нормали будет ![]() . Поэтому переход к другой
стороне поверхности меняет знак поверхностного интеграла второго рода на
противоположный. Другими словами, если поток вектора в направлении внешней
нормали положителен, то в направлении внутренней нормали он будет
отрицательным:
. Поэтому переход к другой
стороне поверхности меняет знак поверхностного интеграла второго рода на
противоположный. Другими словами, если поток вектора в направлении внешней
нормали положителен, то в направлении внутренней нормали он будет
отрицательным: 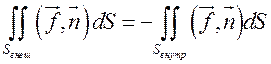 .
.
ПРИМЕР.
Вычислить поток вектора ![]() через внешнюю сторону
эллиптического параболоида
через внешнюю сторону
эллиптического параболоида ![]() (рис.85)
(рис.85)
|
|
Если переписать уравнение параболоида в неявном виде: ![]() или
или ![]() , то
станет ясно, что третья координата нормали к этой поверхности (или вектора
, то
станет ясно, что третья координата нормали к этой поверхности (или вектора ![]() ), имеет постоянный знак, не зависящий от
координат точки, в которой она проведена. При этом внешняя нормаль к данному
параболоиду образует тупой угол с осью
), имеет постоянный знак, не зависящий от
координат точки, в которой она проведена. При этом внешняя нормаль к данному
параболоиду образует тупой угол с осью ![]() (рис.85),
то есть
(рис.85),
то есть ![]() , а
, а ![]() –
единичный круг. Кроме того, левая и правая части параболоида имеют одинаковую
проекцию
–
единичный круг. Кроме того, левая и правая части параболоида имеют одинаковую
проекцию ![]() на координатную плоскость
на координатную плоскость ![]() , но на правой половине
, но на правой половине ![]() , а на левой
, а на левой ![]() . То же
самое верно и для проекции на плоскость
. То же
самое верно и для проекции на плоскость ![]() (рис.85).
Поэтому
(рис.85).
Поэтому
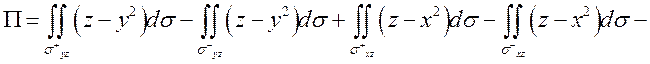
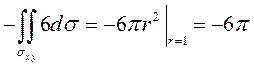 , так как
интегралы по
, так как
интегралы по ![]() и
и ![]() , а
также по
, а
также по ![]() и
и ![]() взаимно
уничтожаются, а
взаимно
уничтожаются, а 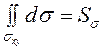 по свойству 1 определенного интеграла.
по свойству 1 определенного интеграла.
ПРИМЕР.
Вычислить поток вектора ![]() через часть плоскости
через часть плоскости ![]() , расположенную в первом октанте, в направлении
нормали, образующей острый угол с осью
, расположенную в первом октанте, в направлении
нормали, образующей острый угол с осью ![]() (рис.86).
(рис.86).
|
Так как ![]() , то на той стороне
плоскости, где угол между нормалью к ней и осью
, то на той стороне
плоскости, где угол между нормалью к ней и осью ![]() –
острый, все направляющие косинусы нормали положительны. Поэтому в соответствии
с формулой (9.12)
–
острый, все направляющие косинусы нормали положительны. Поэтому в соответствии
с формулой (9.12) 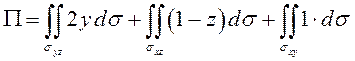 , где
, где ![]() равные
треугольники в плоскостях
равные
треугольники в плоскостях ![]() соответственно (рис.86),
соответственно (рис.86),
![]()
![]() .
.
Так проекции
![]() и
и ![]() равны,
то
равны,
то
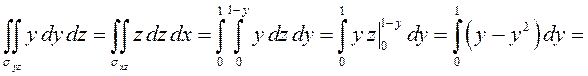
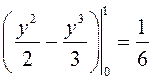 .
.
Следовательно, 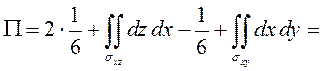
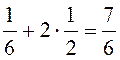 .
.
9.6. Формула Гаусса-Остроградского
Докажем формулу, которая устанавливает связь между
тройным интегралом по замкнутой области ![]() и
интегралом по поверхности
и
интегралом по поверхности ![]() , которая ограничивает
эту область.
, которая ограничивает
эту область.
ТЕОРЕМА (Гаусса-Остроградского). Пусть вектор-функция ![]() непрерывна вместе с частными производными
непрерывна вместе с частными производными
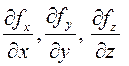 в некоторой правильной ограниченной
замкнутой области
в некоторой правильной ограниченной
замкнутой области ![]() . Тогда имеет место формула
. Тогда имеет место формула
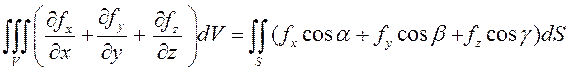 , (9.13)
, (9.13)
где
![]() – поверхность, ограничивающая область
– поверхность, ограничивающая область ![]() , а
, а ![]() –
единичный вектор внешней нормали к
–
единичный вектор внешней нормали к ![]() .
.
Формула (9.13) называется формулой Гаусса–Остроградского.
ДОКАЗАТЕЛЬСТВО.
По условию ![]() правильная область пространства, проекции
которой на координатные плоскости – правильные плоские области. Пусть
поверхность
правильная область пространства, проекции
которой на координатные плоскости – правильные плоские области. Пусть
поверхность ![]() состоит из двух частей (рис. 87).
состоит из двух частей (рис. 87).
|
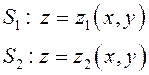 ,
, ![]() .
.
Проведем
внешнюю нормаль к ![]() и обратим внимание на то, что
на верхней части
и обратим внимание на то, что
на верхней части ![]() нормаль образует острый угол с
осью
нормаль образует острый угол с
осью ![]() , значит,
, значит, ![]() . На
нижней части
. На
нижней части ![]()
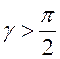 , поэтому
, поэтому ![]() (рис.87).
(рис.87).
Рассмотрим последнее слагаемое в левой части (9.13):
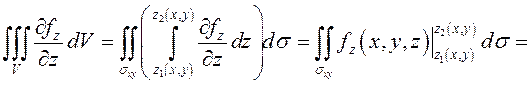
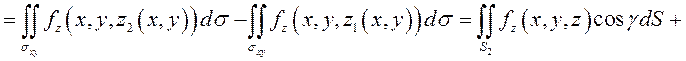
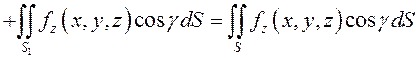
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.