Вычисление двойного интеграла в декартовых координатах. Интеграл Пуассона. Криволинейный и поверхностный интегралы второго рода. Формула Гаусса-Остроградского, страница 9

9.2. Вычисление криволинейного интеграла второго рода

1.  Пусть плоская кривая  задана явно:

.

Тогда согласно определению 

.

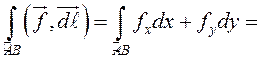
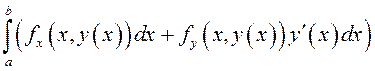Таким образом,

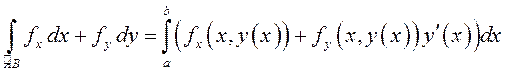.                  (9.1)

Если , то из этой формулы следует, что

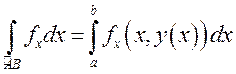                                           (9.2)

2. Пусть плоская кривая  задана параметрически:

.

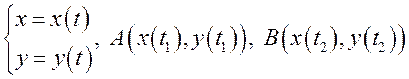В этом  случае

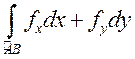
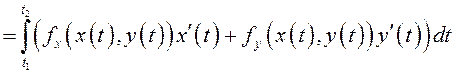.           (9.3)

3. Пусть пространственная кривая  задана параметрически:

.

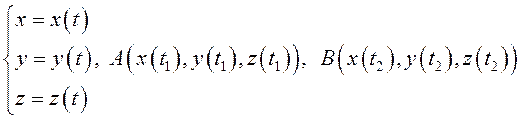В соответствии с определением   

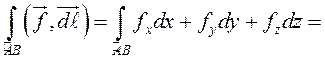
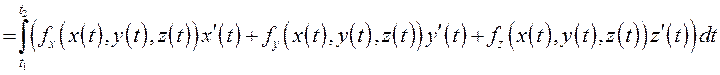  (9.4)

Таким образом, во всех случаях вычисление криволинейного интеграла второго рода сводится к вычислению определенного интеграла на отрезке.

ПРИМЕР. Вычислить 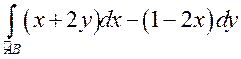, где  – верхняя половина окружности  (рис.75).  

Если записать явное уравнение верхней половины данной окружности , то  нас ожидают очевидные трудности при вычислении определенного интеграла по формуле (9.1).

Поэтому запишем ее параметрическое уравнение, то есть параметризуем данную окружность: 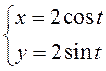. Точке  соответствует значение параметра , а точке  – значение . Теперь по формуле (9.3)

. 

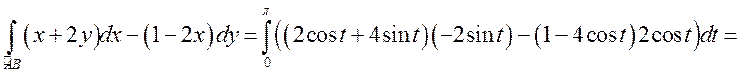
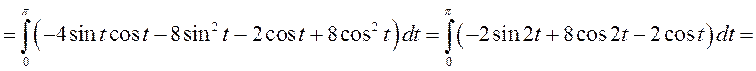
При вычислении последнего определенного интеграла мы воспользовались свойством (8.6).

ПРИМЕР. Вычислить 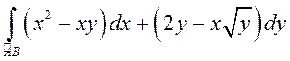, где  – ломаная, соединяющая точки , звенья которой параллельны координатным осям. В соответствии с рис. 76.  

Воспользуемся свойством аддитивности криволинейного интеграла второго рода и вычислим данный интеграл по формуле (9.1):

   .

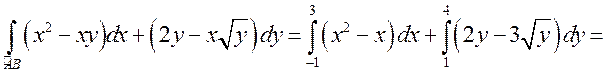
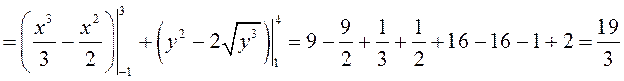9.3. Формула Остроградского-Грина

Формула Остроградского - Грина устанавливает связь между двойным интегралом по некоторой ограниченной плоской области  и криволинейным интегралом по границе  этой области.

ТЕОРЕМА (Остроградского - Грина). Пусть во всех точках правильной плоской области  с кусочно-гладкой границей  определена вектор-функция , непрерывная вместе с частными производными 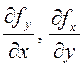. Тогда

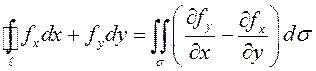                                                    (9.5)

(направление обхода контура  положительно).

Формула (9.5) называется формулой Остроградского-Грина.

ДОКАЗАТЕЛЬСТВО. Вычислим сначала 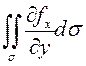. Граница  области  состоит из двух участков (рис.77): кривой , уравнение которой , и  с уравнением . Поэтому

. 

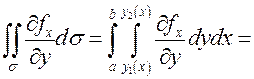
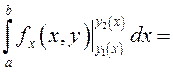
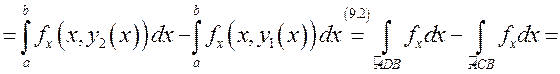
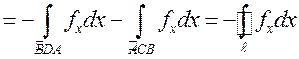Таким образом,                  

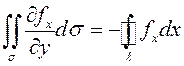                                           (9.6)

Аналогично, если считать теперь, что  состоит из дуг  и  (рис.78), получим:

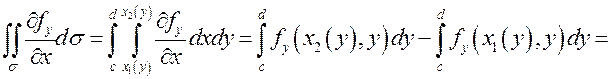
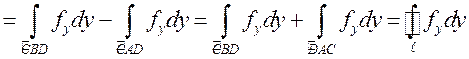, то есть                                 

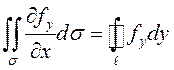                                             .                                               (9.7)

Вычитая из (9.7) равенство (9.6), получим требуемое.

ПРИМЕР. Вычислить 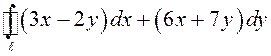, где  задается уравнением  (направление обхода положительно).

Из уравнения контура  после выделения полного квадрата получим , то есть  является окружностью радиуса 1 с центром в точке , поэтому  – круг радиуса 1, площадь которого равна .

Для вычисления интеграла применим формулу Остроградского – Грина (9.5).

;  .

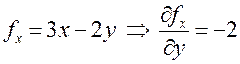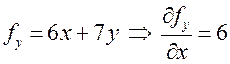Отсюда с учетом свойства 1 определённого интеграла по фигуре

.

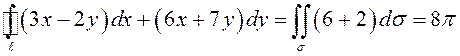9.4. Условия независимости криволинейного интеграла

второго рода от пути интегрирования

ПРИМЕР. Вычислить 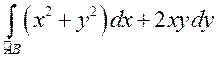 вдоль: а) параболы ,        б) прямой ,   в) ломаной , если  (рис.79).

а) по формуле (9.1)

.      

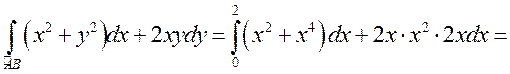
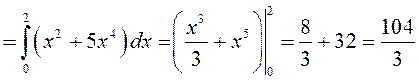б) аналогично .

в)   (рис.79), поэтому

.

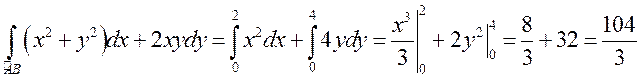Случайным или нет является совпадение результатов вычислений во всех трех случаях? Всегда ли один и тот же криволинейный интеграл, вычисленный вдоль разных путей, принимает одно и то же значение? Это нам предстоит выяснить.