Пусть в каждой точке ![]() пространства
определён вектор скорости течения жидкости
пространства
определён вектор скорости течения жидкости ![]() ,
зависящий от положения точки
,
зависящий от положения точки ![]() и не зависящий от времени.
Вычислим поток через заданную поверхность
и не зависящий от времени.
Вычислим поток через заданную поверхность ![]() , то
есть количество жидкости, протекающей через
, то
есть количество жидкости, протекающей через ![]() за
единицу времени.
за
единицу времени.
Если считать, что ![]() –
плоская площадка, а
–
плоская площадка, а ![]() – вектор, постоянный по величине
и направлению, то за единицу времени частицы жидкости на
– вектор, постоянный по величине
и направлению, то за единицу времени частицы жидкости на ![]() переместятся в направлении
переместятся в направлении ![]() на расстояние
на расстояние ![]() и
попадут на площадку
и
попадут на площадку ![]() (рис.83). Следовательно, поток
будет равен
(рис.83). Следовательно, поток
будет равен ![]() , где
, где ![]() –
плотность жидкости,
–
плотность жидкости, ![]() – высота цилиндра.
– высота цилиндра.
|
Пусть ![]() – единичный вектор
нормали к
– единичный вектор
нормали к 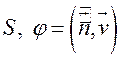 – угол между нормалью и вектором скорости.
– угол между нормалью и вектором скорости.
Тогда
![]() , поэтому, полагая
, поэтому, полагая ![]() ,
получим, что поток
,
получим, что поток ![]() .
.
В общем случае, когда скорость ![]() переменна,
а
переменна,
а ![]() – криволинейная поверхность,
ограниченная замкнутой кривой
– криволинейная поверхность,
ограниченная замкнутой кривой ![]() , полученной формулой
пользоваться нельзя.
, полученной формулой
пользоваться нельзя.
Пусть поверхность ![]() задана
в некоторой прямоугольной декартовой системе координат уравнением
задана
в некоторой прямоугольной декартовой системе координат уравнением ![]() . Если функция
. Если функция ![]() дифференцируема,
то в каждой точке
дифференцируема,
то в каждой точке ![]() этой поверхности вектор
нормали имеет переменное направление, совпадающее с направлением
этой поверхности вектор
нормали имеет переменное направление, совпадающее с направлением ![]() (см. гл. 6), а
(см. гл. 6), а 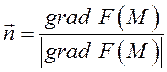 –
единичный вектор нормали.
–
единичный вектор нормали.
Чтобы найти поток, выполним следующие действия:
1)
разобьём поверхность ![]() на
на ![]() достаточно
малых частей
достаточно
малых частей
![]() ,
, ![]() .
.
Так как ![]() – дифференцируемая
функция (то есть в любой точке поверхности
– дифференцируемая
функция (то есть в любой точке поверхности ![]() может
быть проведена касательная плоскость), то можно считать, что каждая часть
может
быть проведена касательная плоскость), то можно считать, что каждая часть ![]() «почти плоская». Кроме того, если вектор
«почти плоская». Кроме того, если вектор ![]() непрерывен, то в пределах малой
поверхности
непрерывен, то в пределах малой
поверхности ![]() он изменяется мало, значит,
он изменяется мало, значит, ![]() имеет приблизительно постоянную величину и
направление,
имеет приблизительно постоянную величину и
направление, ![]() .
.
2) выберем внутри каждой части ![]() произвольную
точку
произвольную
точку ![]() и найдём единичную нормаль
и найдём единичную нормаль ![]() к
к ![]() в точке
в точке
![]() .
.
3) считая, что ![]() , найдем
приближенно поток
, найдем
приближенно поток ![]() через часть поверхности
через часть поверхности ![]() :
: ![]() .
.
4) суммируя все ![]() , найдём
приближенно полный поток через поверхность
, найдём
приближенно полный поток через поверхность ![]() :
: 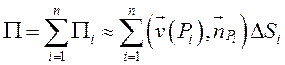 .
.
Чем больше частей ![]() и чем меньше их мера, тем точнее это приближенное
равенство. Поэтому, если существует предел полученной суммы, когда
и чем меньше их мера, тем точнее это приближенное
равенство. Поэтому, если существует предел полученной суммы, когда ![]() при условии, что каждая
при условии, что каждая ![]() стягивается в точку, который не зависит от
способа составления суммы, то естественно принять величину этого предела
равной искомому потоку:
стягивается в точку, который не зависит от
способа составления суммы, то естественно принять величину этого предела
равной искомому потоку: 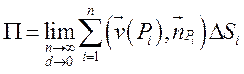 .
.
Можно показать, что если векторы ![]() непрерывны в точках поверхности
непрерывны в точках поверхности ![]() , то этот предел существует. Его называют поверхностным
интегралом второго рода от вектор-функции
, то этот предел существует. Его называют поверхностным
интегралом второго рода от вектор-функции ![]() и
обозначают таким образом:
и
обозначают таким образом: 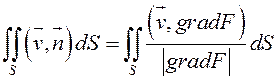 .
.
Итак, поток жидкости через данную поверхность ![]() есть интеграл по этой поверхности от
скалярного произведения
есть интеграл по этой поверхности от
скалярного произведения ![]() , где
, где ![]() – единичная нормаль к поверхности,
– единичная нормаль к поверхности, ![]() – вектор скорости течения жидкости.
– вектор скорости течения жидкости.
Отвлекаясь от физического содержания задачи, можно сформулировать следующее утверждение.
Если во всех точках поверхности ![]() задана непрерывная вектор-функция
задана непрерывная вектор-функция ![]() , то потоком вектора
, то потоком вектора ![]() через эту поверхность называется
поверхностный интеграл второго рода
через эту поверхность называется
поверхностный интеграл второго рода
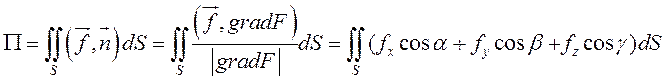 , (9.8)
, (9.8)
где
![]() – направляющие косинусы вектора
– направляющие косинусы вектора ![]() , направленного по нормали к поверхности.
, направленного по нормали к поверхности.
Из этой формулы следует, что вычисление поверхностного интеграла второго рода сводится к вычислению поверхностного интеграла первого рода.
Так как скалярное произведение обладает свойством линейности, а поверхностный интеграл первого рода также линеен и, кроме того, аддитивен, то из формулы (9.8) следует, что поверхностный интеграл второго рода обладает свойствами линейности и аддитивности.
Рассмотрим интеграл 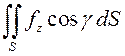 и будем считать, что
и будем считать, что ![]() – острый угол между осью
– острый угол между осью ![]() и нормалью
и нормалью ![]() .
Разрешим неявное уравнение поверхности
.
Разрешим неявное уравнение поверхности ![]() относительно
переменной
относительно
переменной ![]() :
: ![]() , или
, или ![]() – неявное уравнение этой поверхности,
записанное в другой форме. Так как
– неявное уравнение этой поверхности,
записанное в другой форме. Так как 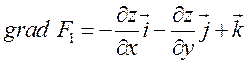 , то
, то
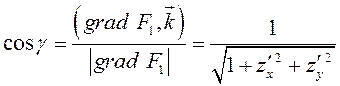 .
.
По
формуле (8.17) ![]() , где
, где ![]() –
элемент проекции поверхности
–
элемент проекции поверхности ![]() на координатную
плоскость
на координатную
плоскость ![]() . Значит,
. Значит,
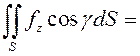
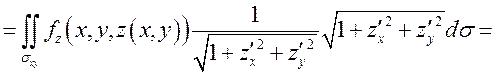
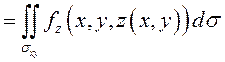 .
.
Если угол ![]() – тупой, то
– тупой, то ![]() и в этом случае
и в этом случае
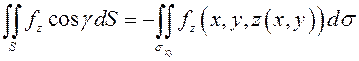 .
(9.9)
.
(9.9)
Аналогично рассмотрим 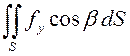 :
перепишем уравнение поверхности в виде
:
перепишем уравнение поверхности в виде ![]()
![]()
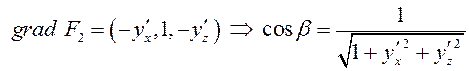 , если
, если
![]() – острый угол между
– острый угол между ![]() и
и ![]() .
.
Спроецируем поверхность ![]() на
координатную плоскость
на
координатную плоскость ![]() и найдем элемент поверхности
и найдем элемент поверхности ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.