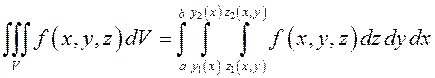 .
.
Так же, как и при вычислении тройного интеграла по
координатному параллелепипеду, этот порядок интегрирования не единственный:
если провести вспомогательные линии, параллельные оси ![]() ,
то внутренний интеграл будет вычисляться по переменной
,
то внутренний интеграл будет вычисляться по переменной ![]() при
фиксированных
при
фиксированных ![]() и
и ![]() , а оставшийся
двойной интеграл – по проекции
, а оставшийся
двойной интеграл – по проекции ![]() области
области ![]() на плоскость
на плоскость ![]() .
.
Тогда
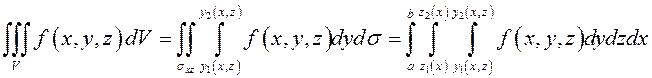 .
.
3. ![]() произвольная пространственная область.
произвольная пространственная область.
Если ![]() не является правильной
областью ни в одном из направлений, то для вычисления тройного интеграла её
следует разбить на части, правильные в направлении какой-либо из координатных
осей, и воспользоваться свойством аддитивности.
не является правильной
областью ни в одном из направлений, то для вычисления тройного интеграла её
следует разбить на части, правильные в направлении какой-либо из координатных
осей, и воспользоваться свойством аддитивности.
ПРИМЕР. Вычислить 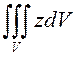 , где
, где ![]()
![]() .
.
Область интегрирования ![]() ограничена
тремя координатными плоскостями и плоскостью
ограничена
тремя координатными плоскостями и плоскостью ![]() .
Напишем уравнение этой плоскости в отрезках:
.
Напишем уравнение этой плоскости в отрезках: 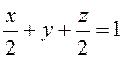 – и
построим область
– и
построим область ![]() . Как видно на рис.62,
. Как видно на рис.62, ![]() – тетраэдр
– тетраэдр ![]() .
.
|
Для вспомогательных линий, параллельных
![]() , поверхностью входа является
, поверхностью входа является ![]() , а поверхностью выхода – плоскость
, а поверхностью выхода – плоскость ![]() или
или
|
|
Проведем
теперь вспомогательные линии, параллельные ![]() : для
них
: для
них ![]() – линия входа, а
– линия входа, а 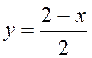 –
линия выхода. В соответствии с этим получим:
–
линия выхода. В соответствии с этим получим:
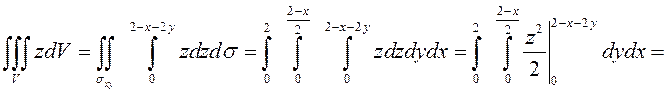
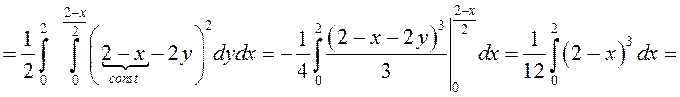
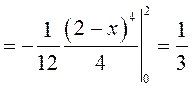 .
.
ЗАМЕЧАНИЕ. Согласно
свойству 1 определенного интеграла объем пространственной области
вычисляется по формуле 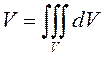 .
.
ПРИМЕР. Вычислить объем области, ограниченной поверхностями ![]() (рис. 64).
(рис. 64).
|
|
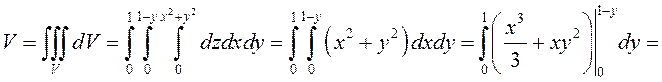
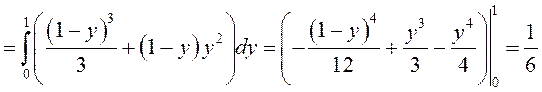 .
.
8.15. Замена переменных в тройном интеграле
1. ВЫЧИСЛЕНИЕ ТРОЙНОГО ИНТЕГРАЛА В ЦИЛИНДРИЧЕСКОЙ СИСТЕМЕ КООРДИНАТ.
Один из способов замены переменных при
вычислении тройного интеграла – переход в цилиндрическую систему координат.
Делать такой переход имеет смысл, когда, например, проекция области
интегрирования ![]() на какую-либо из координатных
плоскостей проще или удобнее описывается в полярных координатах.
на какую-либо из координатных
плоскостей проще или удобнее описывается в полярных координатах.
|
Положение точки |
Координатными поверхностями
цилиндрической системы координат являются ![]() –
плоскость, параллельная
–
плоскость, параллельная ![]() ,
, ![]() – цилиндрическая поверхность с образующей,
параллельной оси
– цилиндрическая поверхность с образующей,
параллельной оси ![]() , и
, и ![]() – плоскость,
проходящая через ось
– плоскость,
проходящая через ось ![]() под углом
под углом ![]() к оси
к оси ![]() (рис.66).
(рис.66).
|
|
Связь между цилиндрическими и декартовыми
координатами точек выражается
формулами: 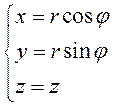 . При вычислении тройного интеграла
в цилиндрических координатах внутренний интеграл всегда берётся по переменной
. При вычислении тройного интеграла
в цилиндрических координатах внутренний интеграл всегда берётся по переменной ![]() , затем – по
, затем – по ![]() и в
последнюю очередь – по
и в
последнюю очередь – по ![]() . Очевидно, что элемент объёма
. Очевидно, что элемент объёма ![]() (см.(8.15)), поэтому формулу перехода от
декартовых координат к цилиндрическим можно записать таким образом:
(см.(8.15)), поэтому формулу перехода от
декартовых координат к цилиндрическим можно записать таким образом:
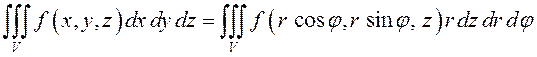 .
.
ПРИМЕР. Вычислить объем области, ограниченной поверхностями
![]() .
.
Уравнение ![]() задает единичную сферу
с центром в начале координат,
задает единичную сферу
с центром в начале координат, ![]() – координатную
плоскость
– координатную
плоскость ![]() , а уравнение
, а уравнение ![]() –
цилиндрическую поверхность (см. гл. 3) с образующей, параллельной оси
–
цилиндрическую поверхность (см. гл. 3) с образующей, параллельной оси ![]() (так как в нем отсутствует переменная
(так как в нем отсутствует переменная ![]() ). Чтобы выяснить, какая кривая является
направляющей для этой поверхности, перепишем ее уравнение в цилиндрических
координатах:
). Чтобы выяснить, какая кривая является
направляющей для этой поверхности, перепишем ее уравнение в цилиндрических
координатах: ![]() . Так как уравнение
цилиндрической поверхности одновременно является и уравнением ее направляющей,
то это, очевидно, лемниската Бернулли (рис.67).
. Так как уравнение
цилиндрической поверхности одновременно является и уравнением ее направляющей,
то это, очевидно, лемниската Бернулли (рис.67).
|
Мы будем вычислять объем по формуле 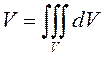 в цилиндрических координатах, поэтому
необходимо переписать и уравнение сферы:
в цилиндрических координатах, поэтому
необходимо переписать и уравнение сферы: ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.