Вычисление двойного интеграла в декартовых координатах. Интеграл Пуассона. Криволинейный и поверхностный интегралы второго рода. Формула Гаусса-Остроградского, страница 2

На рис. 44 область  – правильная в направлении  и неправильная в направлении ;  – правильная в направлении  и неправильная в направлении ;  – правильная, а  – неправильная область в декартовых координатах.

Пусть  – правильная  область  в  системе  координат    с границей  (рис.45). Крайняя левая точка  и крайняя правая точка  делят границу  на две части:  и .

Если провести вспомогательные прямые, параллельные оси , то для них  – линия входа, а  – линия выхода. В этом случае  .

На эту же область можно посмотреть иначе: пусть точка  – крайняя нижняя, а точка крайняя верхняя точки границы  (рис 46). Они делят  на две части:  и .

Проведем вспомогательные линии параллельно оси . Они входят в область на кривой , а выходят из неё на . Поэтому этот же двойной интеграл сведется к повторному другим способом: .

ЗАМЕЧАНИЕ. В декартовой системе координат повторный интеграл всегда имеет постоянные пределы интегрирования во внешнем интеграле и, как правило, переменные пределы во внутреннем. Постоянными пределы интегрирования внутреннего интеграла будут, лишь если   – координатный прямоугольник.

Рассмотрим пример, который поможет лучше понять, как расставлять пределы интегрирования в повторном интеграле и, соответственно, выбирать оптимальный порядок интегрирования (в тех случаях, когда он существует).

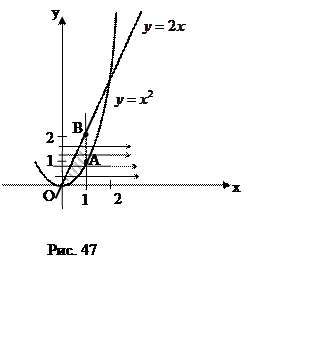ПРИМЕР. Изменить порядок интегрирования в интеграле

Во-вторых, по условию нужно изменить порядок интегрирования, то есть вычислить внутренний интеграл по , а внешний – по . Чтобы не ошибиться, расставляя новые пределы интегрирования, надо провести вспомогательные линии. В этом случае они должны пересекать область параллельно оси .Для таких прямых, как видно из рис.47, одна линия входа в область и две линии выхода, поэтому двойной интеграл сведется не к одному, а к двум повторным интегралам (в соответствии со свойством аддитивности двойного интеграла).

Найдем координаты точек пересечения линий, ограничивающих :

.

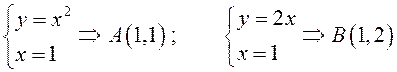Кроме того, если , то  при ; если  , то .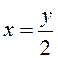

Итак,               

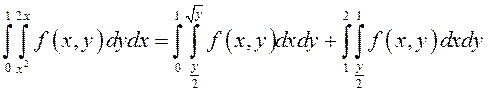               (8.14)

Таким образом, при вычислении двойного интеграла по  данной области  (рис.47) первоначальный порядок интегрирования является более оптимальным, так приводит к одному повторному интегралу.

Заметим, что обе части равенства (8.14) соответствуют одному двойному интегралу, хотя в правой части (8.14) – два повторных интеграла.

ПРИМЕР. Вычислить площадь области, ограниченной линиями 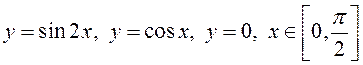 (рис. 48).

По определению двойного интеграла (см. свойство 1) площадь плоской области  .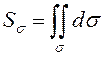

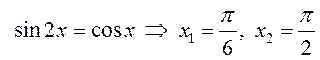Найдем точку пересечения кривых  и   при  .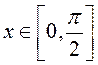        

В этом двойном интеграле можно перейти к повторному двумя способами. Проведя вспомогательные прямые параллельно , получим:   

.

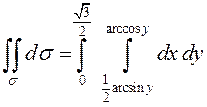Если провести вспомогательные линии параллельно , то  

.

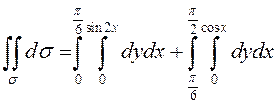Несмотря на то, что во втором случае получилось два повторных интеграла, первый способ вычисления этой площади, более сложный из-за более трудоемкого нахождения первообразной во внешнем интеграле. Поэтому, выбирая порядок интегрирования в двойном интеграле, необходимо учитывать не только конфигурацию области , но и особенности подынтегральной функции.

Итак,

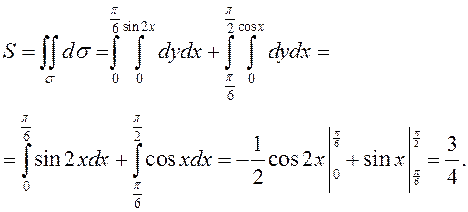
5. произвольная плоская область.