Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
«Омский государственный технический университет»
Транспортная задача. Матричные игры.
Методические указания для студентов экономических
специальностей
Омск -2007
Составители: Соколовский Мирон Наумович, доцент
Печатается по решению редакционно-издательского совета
Омского государственного технического университета
Редактор
ИД___________ от ___________
Подписано в печать . Бумага офсетная. Формат 60х84 1/16
Отпечатано на дупликаторе. Усл. печ. л. . Уч.-изд. л. .
Тираж 100 экз. Заказ .
__________________________________________________________
Издательство ОмГТУ. 644050, г. Омск, пр-т Мира, 11
Типография ОмГТУ
Транспортная задача
Транспортная задача (ТЗ) является примером экономической задачи, приводящей к модели линейного программирования (ЛП), и формулируется следующим образом.
Имеется ![]() пунктов
пунктов ![]() производства однородного продукта
(например, угля), объем производства в пункте
производства однородного продукта
(например, угля), объем производства в пункте ![]() составляет
составляет
![]() единиц. Продукт потребляется в
единиц. Продукт потребляется в ![]() пунктах
пунктах ![]() потребность
в пункте
потребность
в пункте ![]() составляет в
составляет в ![]() единиц.
Предполагается , что суммарный объём производства совпадает с суммарной потребностью
единиц.
Предполагается , что суммарный объём производства совпадает с суммарной потребностью
![]() (1)
(1)
(условие баланса).Стоимость
перевозки одной единицы продукта из ![]() в
в ![]()
равна ![]() Требуется составить план перевозок из пунктов
Требуется составить план перевозок из пунктов
![]() в пункты
в пункты ![]() так,
чтобы вывезти из каждого пункта
так,
чтобы вывезти из каждого пункта ![]() весь запас продукта,
полностью удовлетворить потребность в каждом из пунктов
весь запас продукта,
полностью удовлетворить потребность в каждом из пунктов ![]() и минимизировать транспортные расходы.
Для наглядности представим условия ТЗ в виде таблицы, строкам которой
соответствуют пункты производства
и минимизировать транспортные расходы.
Для наглядности представим условия ТЗ в виде таблицы, строкам которой
соответствуют пункты производства ![]() , а столбцам – пункты
потребления
, а столбцам – пункты
потребления ![]() :
:
Таблица 1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В
клетке ![]() таблицы 1 записаны соответствующая
стоимость перевозки
таблицы 1 записаны соответствующая
стоимость перевозки ![]() (правый верхний угол) и переменная
(правый верхний угол) и переменная
![]() (в центре клетки), смысл
(в центре клетки), смысл ![]() - планируемый объем перевозки из
- планируемый объем перевозки из ![]() в
в ![]() .
Справа от каждой строки и под каждым столбцом записаны соответствующие запасы
.
Справа от каждой строки и под каждым столбцом записаны соответствующие запасы ![]() и потребности
и потребности ![]()
План
ТЗ представляет собой матрицу 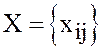 размера
размера ![]() При плане
При плане 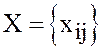 расходы
на перевозку из
расходы
на перевозку из ![]() в
в ![]() равны
равны
![]() а общая стоимость всех перевозок – сумме
этих выражений по всем клеткам таблицы 1. Требования вывоза всех запасов и
удовлетворения всех потребностей означают, что сумма всех
а общая стоимость всех перевозок – сумме
этих выражений по всем клеткам таблицы 1. Требования вывоза всех запасов и
удовлетворения всех потребностей означают, что сумма всех ![]() в
в ![]() строке
(
строке
(![]() столбце) равна
столбце) равна ![]() Таким
образом, математическая модель ТЗ имеет вид
Таким
образом, математическая модель ТЗ имеет вид
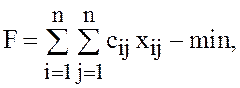 (2)
(2)
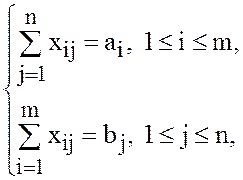 (3)
(3)
![]() (4)
(4)
то есть является задачей ЛП в канонической форме и может быть решена симплекс-методом. Основная идея симплекс-метода заключается в построении последовательности «улучшающихся» опорных планов, в которой последний план – оптимальный. При решении задачи ЛП общего вида планы последовательности представляются симплексными таблицами, то есть различными формами записи системы уравнений из условия задачи. В транспортной задаче система (3) имеет очень простую структуру. Использование особенностей системы (3) позволяет заменить симплексные таблицы на другой способ представления опорных планов, опорные таблицы ТЗ, и существенно упростить как нахождение начального плана, так и переход от текущего плана к следующему.
При
условии (1) система (3) ![]() уравнений с
уравнений с ![]() неизвестными совместна –
числа
неизвестными совместна –
числа ![]() образуют одно из её решений (проверьте!).
Для определения ранга (числа независимых уравнений) системы заметим, что
результатом сложения уравнений, соответствующих всем строкам таблицы 1,
будет
образуют одно из её решений (проверьте!).
Для определения ранга (числа независимых уравнений) системы заметим, что
результатом сложения уравнений, соответствующих всем строкам таблицы 1,
будет
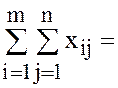 (сумма всех
(сумма всех ![]() )
)![]()
и это
же уравнение получается при сложении всех уравнений, соответствующих столбцам.
Отсюда ![]() уравнений (3) зависимы, более того,
каждое из них является следствием
уравнений (3) зависимы, более того,
каждое из них является следствием ![]() остальных. С другой стороны,
рассмотрим какие-нибудь
остальных. С другой стороны,
рассмотрим какие-нибудь ![]() уравнений из (3),
например, результат удаления уравнения
уравнений из (3),
например, результат удаления уравнения ![]() соответствующего
1-ой строке таблицы 1. При любом
соответствующего
1-ой строке таблицы 1. При любом ![]() переменная
переменная ![]() входит только в одно из этих
входит только в одно из этих ![]() , уравнений – то, которое соответствует
, уравнений – то, которое соответствует ![]() ому столбцу таблицы 1. Используя это
свойство легко проверить, что никакое из
ому столбцу таблицы 1. Используя это
свойство легко проверить, что никакое из ![]() рассматриваемых
уравнений не является следствием
рассматриваемых
уравнений не является следствием ![]() остальных. Аналогично
доказывается независимость любых
остальных. Аналогично
доказывается независимость любых ![]() уравнений из (3).
уравнений из (3).
Таким
образом, система (3) имеет ранг ![]() и, следовательно,
любой базис системы [1,
стр.18], содержит
и, следовательно,
любой базис системы [1,
стр.18], содержит ![]() переменную. Напомним, что любой опорный
план задачи ЛП, [1, стр.20],
порождается некоторым базисом и все свободные
(небазисные) переменные этого плана равны нулю. В случае вырожденной
задачи ЛП, [1, стр.26],
который возможен и для ТЗ (см. упражнение
2), существуют опорные планы с нулевыми значениями не только всех свободных,
но и некоторых базисных переменных. Вырожденный опорный план может порождаться
несколькими различными базисами.
переменную. Напомним, что любой опорный
план задачи ЛП, [1, стр.20],
порождается некоторым базисом и все свободные
(небазисные) переменные этого плана равны нулю. В случае вырожденной
задачи ЛП, [1, стр.26],
который возможен и для ТЗ (см. упражнение
2), существуют опорные планы с нулевыми значениями не только всех свободных,
но и некоторых базисных переменных. Вырожденный опорный план может порождаться
несколькими различными базисами.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.