Транспортная задача. Матричные игры: Методические указания к практическим занятиям, страница 9

          Замечание 2. При применении метода потенциалов к вырожденной ТЗвозможно  зацикливание,  см. [1, стр.27].Уточнение алгоритма метода потенциалов, позволяющее избежать зацикливания, выходят за рамки данных указаний.

Открытая модель ТЗ. Задача (2) – (4) называется закрытой моделью ТЗ,  в этой модели предполагается выполнение условия баланса (1). Открытая модель ТЗ представляет собой математическую постановку задачи минимизации транспортных расходов в ситуации, когда условие баланса нарушено. Открытая модель отличается от закрытой только тем, что в одной из групп ограничений (3), соответствующих строкам или столбцам таблицы 1, уравнения заменяются на неравенства. Если суммарный запас в пунктах производства больше суммарной потребности в пунктах потребления,

                                 (1а)

ограничения (3)   закрытой модели заменяются на ограничения

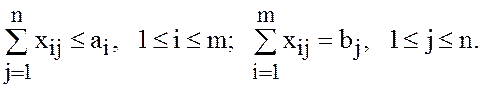                (3а)

Если суммарный запас меньше суммарной потребности,

                                (1б)

ограничения (3) заменяются на ограничения

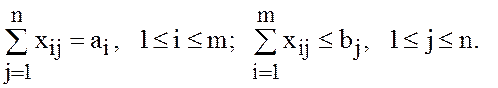                     (3б)

Объяснение содержательного смысла ограничений (3а) и (3б) предоставляется читателю.

Открытая модель ТЗ сводится к закрытой введением дополнительного фиктивного пункта потребления     в случае (1а) или  фиктивного пункта производства    в случае (1б). Покажем на конкретном примере, как это делается.

Пример 6. Найти оптимальный план ТЗ, представленной таблицей а) на рис. 8.

Рис. 8

Решение: В данной ТЗ        условие баланса  нарушено, запасы больше потребностей на 37-33=4 единицы.  Введём дополнительный фиктивный  пункт потребления   в который будут  «свозиться» эти излишки запасов, т.е. положим

Поскольку на самом деле пункт потребления   не существует и никакие перевозки в этот пункт не осуществляются, стоимости перевозок   равны нулю. Таким образом исходная открытая модель преобразуется в закрытую, представленную таблицей б) на рис. 8. Описанное выше преобразование фактически является известным способом перехода к  канонической  форме задачи ЛП  с помощью  балансовых переменных    [1,cтр. 7, последний абзац],  содержательный смысл переменной   «невывезенная» (оставшаяся на складе) часть запаса продукта в пункте производства 

Результат решения закрытой ТЗ методом потенциалов представлен на рис. 8в) ( проверьте выполнение признака оптимальности). В оптимальном плане исходной задачи   стоимость перевозок   остатки запасов продукта в пунктах    равны     единиц соответственно.

В примере 6 рассматривалась открытая ТЗ, удовлетворяющая условию (1а). При сведении к закрытой модели задач, удовлетворяющих (1б), вводится фиктивный пункт производства  с запасом                      и стоимостями перевозок

содержательный  смысл балансовой переменной    в этом случае – «недопоставка» продукта в пункт потребления 

          Задача о назначениях. К транспортной модели (2)-(4) сводится задача  о назначениях, которая формулируется следующим образом.