Транспортная задача. Матричные игры: Методические указания к практическим занятиям, страница 11

где   Доказать, что задача вырождена. У к а з а н и е. Рассмотреть две «подзадачи» исходной ТЗ:   первая – с производителями     и потребителями   вторая – с производителями   и потребителями    Для каждой из подзадач построить начальную опорную таблицу  с   и     занятыми клетками соответственно.

3. Решить методом потенциалов ТЗ из упражнения 1.

4. Найти все оптимальные планы следующих ТЗ:

5. Решить следующие ТЗ с открытой моделью:

6. Доказать, что а) при целых значениях всех запасов    и потребностей    начальный опорный план ТЗ, построенный  методом СЗУ  или МС, является целочисленным (все  целые числа);  б)  перестройка по циклу сохраняет свойство целочисленности опорного плана.

7. Решить задачи о назначениях с заданными  матрицами затрат:

Матричные  игры

В различных видах практической деятельности часто возникают ситуации, в которых интересы отдельных лиц (сторон) не совпадают или даже прямо противоположны. В таких конфликтных ситуациях эффективность решений, принимаемых каждой из сторон, зависит от действий других участников. При этом, как правило, каждая из сторон вынуждена действовать  в условиях неопределенности, не зная заранее, какие решения будут приняты другими.

Модели конфликтных ситуаций и различные подходы к определению «разумного» поведения сторон в условиях неопределенности изучаются математической  теорией, получившей название теория игр. Математическая модель конфликтной ситуации называется  игрой, участники конфликта - игроками. Мы будем рассматривать только игры двух лиц с нулевой суммой (антагонистические игры). В конкретной игре двух лиц с нулевой суммой между игроками  А  и  В считаются  заданными

- два множества    и    всех возможных  стратегий (способов действий) игроков  А  и В  соответственно;

- платежная  функция     с действительными значениями (любого знака), определенная на каждой  паре стратегий 

Исход (результат) игры определяется выбором одной из своих возможных стратегий каждым игроком. В игре с нулевой суммой выигрыш игрока А совпадает с проигрышем игрока В и  равен  где     и  стратегии, выбранные игроками (в данной «партии» игры). Цель игрока А - максимизировать свой выигрыш, цель игрока В – минимизировать выигрыш игрока А, т.е.  свой проигрыш.

Конечные игры. Рассмотрим игру двух лиц с нулевой суммой, в которой множества возможных стратегий игроков  А и В  конечны  и имеют мощности   и    соответственно. Обозначим   стратегии игрока А; стратегии игрока В. В такой конечной игре  значения платежной  функции 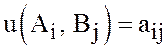   образуют матрицу  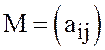  размера   которая называется платежной матрицей или  просто матрицей игры. Строки  соответствуют стратегиям игрока А, столбцы – стратегиям игрока В.