Соответствующая
пара стратегий ![]() также называется седловой. Справедлива
следующая
также называется седловой. Справедлива
следующая
Теорема
о седловой точке. Пара стратегий ![]() является
решением игры тогда и только тогда, когда эта пара седловая. Конечная игра
имеет решение тогда и только тогда, когда платёжная матрица содержит (хотя бы
один) седловой элемент.
является
решением игры тогда и только тогда, когда эта пара седловая. Конечная игра
имеет решение тогда и только тогда, когда платёжная матрица содержит (хотя бы
один) седловой элемент.
Доказательство:Утверждение
«![]() - решение игры» по определению
эквивалентно выполнению трёх равенств
- решение игры» по определению
эквивалентно выполнению трёх равенств
![]() (23)
(23)
Вторая часть утверждения теоремы следует из первой. Для доказательства первой части достаточно проверить, что каждая из систем равенств (22) и (23) является следствием другой.
Из
равенств (23) и определений величин ![]() и
и ![]() следует, что
следует, что
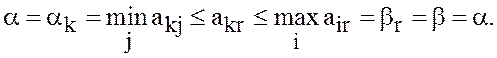
В
этой цепочке крайние числа совпадают (равны ![]() ),
поэтому оба неравенства обращаются в равенства и
),
поэтому оба неравенства обращаются в равенства и ![]() т.е.
выполнены равенства (22).
т.е.
выполнены равенства (22).
Наоборот, пусть выполнены равенства (22). Тогда
![]()
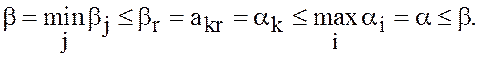
Здесь, кроме (22), использованы определения чисел ![]() и
и ![]() и неравенство (19); как
и в предыдущей цепочке, все неравенства обращаются в равенства и,
следовательно,
и неравенство (19); как
и в предыдущей цепочке, все неравенства обращаются в равенства и,
следовательно, ![]() т.е. выполнены равенства (23).
Из доказательства теоремы следует также, что все седловые элементы платёжной
матрицы совпадают между собой и равны цене игры
т.е. выполнены равенства (23).
Из доказательства теоремы следует также, что все седловые элементы платёжной
матрицы совпадают между собой и равны цене игры ![]() (если,
конечно, такие элементы существуют).
(если,
конечно, такие элементы существуют).
В
качестве упражнения предлагаем читателю проверить справедливость доказанной
теоремы в примерах 8 и 9: в первом случае матрицы ![]() и
и ![]()
не
содержат седловых элементов, во втором решениям игры ![]() и
и
![]() соответствуют седловые элементы
соответствуют седловые элементы ![]()
Смешанные
стратегии. В конечной игре без седловых точек (т.е. при ![]() ) у игроков нет оптимальных стратегий, а
игрок, «угадавший» выбор противника, получает большое преимущество. Пусть,
например, игрок
) у игроков нет оптимальных стратегий, а
игрок, «угадавший» выбор противника, получает большое преимущество. Пусть,
например, игрок ![]() знает, что
знает, что ![]() выбрал
выбрал ![]() Тогда
Тогда
![]() может применить стратегию
может применить стратегию ![]() , соответствующую наибольшему элементу
, соответствующую наибольшему элементу ![]() го столбца платежной матрицы, и выиграть
го столбца платежной матрицы, и выиграть
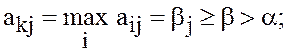 этот результат, конечно, вполне устраивает
игрока
этот результат, конечно, вполне устраивает
игрока ![]() и невыгоден игроку
и невыгоден игроку ![]() . Понятно, что в такой ситуации каждый
игрок стремится скрыть свой окончательный выбор и в то же время разведать
намерения противника. Любые рассуждения игрока, стремящегося засекретить свой
выбор, могут быть восстановлены разумным противником, которому
известны правила игры. Естественный способ сделать собственный выбор
непредсказуемым состоит в том, чтобы сделать его случайным.
. Понятно, что в такой ситуации каждый
игрок стремится скрыть свой окончательный выбор и в то же время разведать
намерения противника. Любые рассуждения игрока, стремящегося засекретить свой
выбор, могут быть восстановлены разумным противником, которому
известны правила игры. Естественный способ сделать собственный выбор
непредсказуемым состоит в том, чтобы сделать его случайным.
Представим себе, что конечная игра повторяется много раз и игроков интересует не выигрыш в каждой отдельной партии, а средний выигрыш по многим партиям; такой средний выигрыш зависит, очевидно, от того, насколько часто игроки используют каждую из своих стратегий.
Смешанной стратегией
игрока ![]() называется вектор
называется вектор
![]() где
где
![]() Здесь координата
Здесь координата ![]() понимается
как вероятность (или частота) применения стратегии
понимается
как вероятность (или частота) применения стратегии ![]() Аналогично вводится понятие смешанной
стратегии
Аналогично вводится понятие смешанной
стратегии ![]() игрока
игрока ![]() ,
,
![]() где
где ![]()
Игра в смешанных стратегиях заключается в следующем. Игроки ![]() и
и ![]() выбирают
(независимо друг от друга) определенные смешанные стратегии
выбирают
(независимо друг от друга) определенные смешанные стратегии ![]() и
и ![]() соответственно.
Затем игрок
соответственно.
Затем игрок ![]() организует лотерею, в которой стратегии
организует лотерею, в которой стратегии ![]() выпадают с вероятностями
выпадают с вероятностями ![]() а игрок
а игрок ![]() -
лотерею, в которой
-
лотерею, в которой ![]() выпадают с вероятностями
выпадают с вероятностями ![]() Выигрыш игрока
Выигрыш игрока ![]() совпадает
с проигрышем игрока
совпадает
с проигрышем игрока ![]() и представляет собой случайную
величину, для которой возможные значения
и представляет собой случайную
величину, для которой возможные значения ![]() имеют
вероятности
имеют
вероятности ![]()
Платёжная функция ![]() игры в смешанных стратегиях определяется
как математическое ожидание (среднее значение) этой случайной величины
и, следовательно,
игры в смешанных стратегиях определяется
как математическое ожидание (среднее значение) этой случайной величины
и, следовательно,
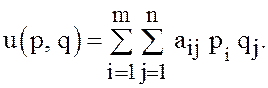 (24)
(24)
В теории игр переход к случайному выбору стратегий называется смешанным расширением игры, стратегии исходной игры называются чистыми. а сама исходная игра – игрой в чистых стратегиях.
Чистой
стратегии ![]() поставим в соответствие смешанную
стратегию
поставим в соответствие смешанную
стратегию ![]() где число 1 стоит на
где число 1 стоит на ![]() ом месте: применение
ом месте: применение ![]() заключается в выборе
заключается в выборе ![]() с вероятностью 1, т.е. во всех партиях.
Аналогично связаны
чистая стратегия
с вероятностью 1, т.е. во всех партиях.
Аналогично связаны
чистая стратегия ![]() и смешанная стратегия
и смешанная стратегия ![]()
где
число 1 стоит на ![]() ом месте. Из формулы (24)
следует, что
ом месте. Из формулы (24)
следует, что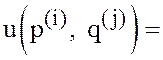
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.