Транспортная задача. Матричные игры: Методические указания к практическим занятиям, страница 3

Требуется:  1) убедиться, что все четыре таблицы являются  таблицами ТЗ и найти значения     целевых функций (транспортных  расходов)  для соответствующих допустимых планов;   2) указать, какие из таблиц ТЗ являются опорными, какие представляют опорные  планы;   3) в таблице г) построить цикл, в котором  (1, 3) – единственная незанятая клетка.

Решение.  1) Все таблицы заполнены только неотрицательными числами, их суммы в строках и столбцах равны соответствующим запасам или потребностям – все требования к таблицам ТЗ выполнены. Для таблицы а)

Аналогично находим    

2) В опорных таблицах должно быть    занятых клеток. Таблицы  а)   и  б) – не опорные, т.к. в них заняты    и     клеток,  соответственно. В таблице в)  занято 6  клеток, но существует цикл, в котором  все клетки заняты (изображён на рис. 2в), по теореме 1 эта таблица не опорная. В таблице г)  из шести занятых клеток (или их части)  нельзя образовать цикл (проверьте!), по теореме  1 она является опорной.

Таблица а)  представляет  не опорный план, т. к.  в нем    положительных    значений      таблица г) представляет опорный план, как и любая опорная таблица.  Таблицы б)  и  в)  также  представляют опорные планы, т. к. их можно превратить в опорные таблицы ТЗ, не меняя представляемого ими плана: для б)  достаточно заполнить числом 0 клетку (1, 1)  (есть и другие варианты, какие?), для в) – перенести 0 из клетки  (3, 1)  в любую незанятую (почему?). Заметим, что в занятых клетках каждой из таблиц б),  в)   и г) всего пять положительных    чисел, и, следовательно, все эти таблицы представляют  вырожденные  опорные планы.

3) В  искомом цикле должно быть горизонтальное звено,  соединяющее (1, 3)  с одной из занятых клеток 1-й строки, т. е.  с (1, 1)  или (1, 4). Но из (1, 4)  нельзя провести следующее, вертикальное звено, т. к. в 4-ом столбце нет других занятых клеток. Из клетки  (1, 1)  можно провести вертикальное звено в  (3, 1), затем,  чередуя  горизонтальные и вертикальные звенья, пройти через клетки  (3, 2),  (2, 2),  (2, 3)  и вернуться в (3, 1) - на всех шагах следующее звено выбирается однозначно. Искомый цикл построен  и очевидна его  единственность, т.е.  получено подтверждение справедливости теоремы 2 в данном частном случае.

Построение начальной опорной таблицы. По теореме 1 в опорной таблице ТЗ занятые клетки и записанные в них неотрицательные числа выбраны так, что а) сумма чисел в занятых клетках любого ряда совпадает с соответствующим   значением     или     (это просто определение таблицы ТЗ);

б) число занятых клеток равно

в) любой цикл таблицы содержит хотя бы одну незанятую клетку.

Будем выбирать занятые клетки искомой таблицы и заполнять их  неотрицательными   числами постепенно, шаг за шагом, по одной клетке на каждом шаге.  Пусть     и  клетка и число, выбранные на ом шаге,  В процессе заполнения каждому шагу соответствуют определенные значения  невязок  строк и столбцов,

(сумма чисел  ой строки после го шага), 

(сумма чисел  ого столбца после го шага), 

В начале процесса все клетки  незаняты  и

                               (5)

После очередного шага любая невязка сохраняет  своё  прежнее  значение  или уменьшается, так как при     по определению

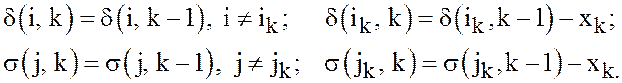         (6)

Если    (такое возможно в вырожденных ТЗ), сохраняются значения всех  невязок, при    уменьшаются невязки   ой строки и  го столбца. Очевидно, что при любом    сумма невязок  го шага по строкам совпадает с суммой невязок  го шага по столбцам (условие баланса невязок, сравните с (1)).

Свойства  а)   и  б)  опорных таблиц  ТЗ эквивалентны требованиям  «на последнем шаге все невязки равны нулю» и  «процесс  заполнения заканчивается на  ом  шаге», т.е. системе    равенств

        (7)

Покажем, как надо выбирать клетки   и числа    чтобы в конце процесса выполнялись свойства   а),   б)  и  в).

На первом шаге выберем     произвольно и запишем в неё число    равное меньшему  из  чисел    или   Из начальных условий (5) и равенств (6) следует, что    и все невязки 1-го шага неотрицательны, а хотя бы одна из невязок      (возможно обе)  равна 0. Выделим  ую строку или ый столбец – тот из этих двух рядов, в котором невязка 1-го шага равна 0.