9. Каким
ограничениям должны удовлетворять числа ![]() и
и ![]() чтобы пара чистых стратегий
чтобы пара чистых стратегий ![]() была седловой в следующих играх а)
была седловой в следующих играх а) 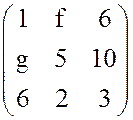 б)
б) 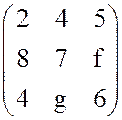
10. Доказать,
что пара смешанных стратегий 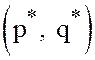 является решением
игры с матрицей
является решением
игры с матрицей ![]() и найти цену игры
и найти цену игры
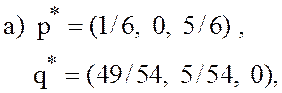
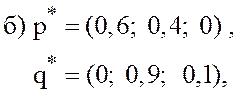
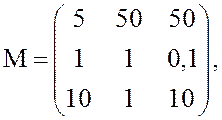
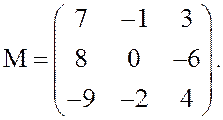
У к а з а н и е.Вычислить
гарантированный выигрыш 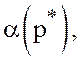 гарантированный проигрыш
гарантированный проигрыш 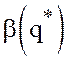 по формулам (30) и убедиться, что
по формулам (30) и убедиться, что 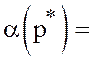
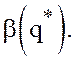
11. По графикам ![]() гарантированных
выигрышей игрока
гарантированных
выигрышей игрока ![]() двух игр размера
двух игр размера ![]()
|
8
4 2
-1 -2 |
7 5 3
1 0,5
0,8 |
записать платежные матрицы этих игр. Доказать, что: первая игра имеет цену
![]() а её решением будет пара чистых
стратегий
а её решением будет пара чистых
стратегий ![]() то есть
то есть ![]()
![]() вторая игра имеет цену
вторая игра имеет цену ![]() решениями игры будут пары
решениями игры будут пары 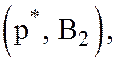 где
где 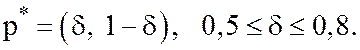
12.Сократить
платёжную матрицу и найти решение и цену игры графическим методом а) 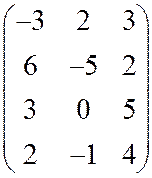 б)
б)
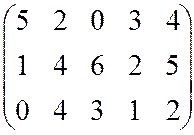 в)
в) 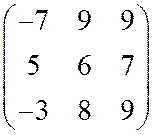 г)
г)
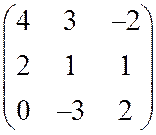
13. Найти все решения и цену игры с матрицей
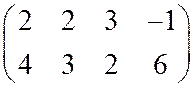
У
к а з а н и е.Через точку ![]() с наибольшей ординатой
с наибольшей ординатой
![]() на ломаной
на ломаной ![]() проходят
три прямые с угловыми коэффициентами
проходят
три прямые с угловыми коэффициентами ![]() Парам
чистых стратегий
Парам
чистых стратегий ![]() и
и ![]() соответствуют
две различные минимаксные смешанные стратегии
соответствуют
две различные минимаксные смешанные стратегии ![]() и
и ![]() все выпуклые линейные комбинации
все выпуклые линейные комбинации ![]() этих стратегий также будут
минимаксными.
этих стратегий также будут
минимаксными.
14.
Показать, что в примере 13 нельзя переходить к задачам ЛП без «сдвига»
элементов матрицы ![]() так как задачи (36-37) и
(38-39), составленные непосредственно по матрице
так как задачи (36-37) и
(38-39), составленные непосредственно по матрице ![]() неразрешимы: в
первой из них целевая функция не ограничена сверху (смотри пример 9 в [1]),
а во второй нет допустимых планов (аналогичное утверждение верно для любой
матричной игры, в которой
неразрешимы: в
первой из них целевая функция не ограничена сверху (смотри пример 9 в [1]),
а во второй нет допустимых планов (аналогичное утверждение верно для любой
матричной игры, в которой ![]() ).
).
15. Найти решения и цены следующих игр методом ЛП:
а)  б)
б)  в)
в)
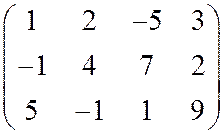
16.
(Игра «раз-два-три»). Каждый игрок выбирает одно из трёх чисел
(стратегий) «раз», «два», или «три». Выигрыш игрока ![]() равен выбранному им числу, если оно
совпадает с выбором противника, и нулю в противном случае. Найти гарантирующие
чистые стратегии, решение и цену игры в смешанных стратегиях.
равен выбранному им числу, если оно
совпадает с выбором противника, и нулю в противном случае. Найти гарантирующие
чистые стратегии, решение и цену игры в смешанных стратегиях.
17.
(Угадай 1 или 2). Каждый игрок выбирает число 1 или 2 и одновременно
пытается угадать выбор противника. Если только один игрок угадал правильно, его
выигрыш равен сумме чисел, выбранных обоими игроками, во всех остальных случаях
игра заканчивается вничью: (выигрыш ![]()
![]() (про-игрыш
(про-игрыш
![]()
![]() . Найти решение и цену
игры. У к а з а н и я: 1)
каждый игрок имеет четыре чистые
стратегии вида
. Найти решение и цену
игры. У к а з а н и я: 1)
каждый игрок имеет четыре чистые
стратегии вида ![]() задуманное число,
задуманное число, ![]() предполагаемый ответ противника; 2) в
матрице игры
предполагаемый ответ противника; 2) в
матрице игры ![]() (кососимметрическая матрица),
вектор
(кососимметрическая матрица),
вектор ![]() максиминная смешанная стратегия тогда и
только тогда, когда
максиминная смешанная стратегия тогда и
только тогда, когда ![]() минимаксная стратегия; 3) задача ЛП, к которой сводится игра, имеет бесконечное
множество оптимальных планов, смотри пример 8 в [1].
минимаксная стратегия; 3) задача ЛП, к которой сводится игра, имеет бесконечное
множество оптимальных планов, смотри пример 8 в [1].
18. Противники ![]() и
и ![]() ведут
борьбу за два стратегических пункта. В распоряжении
ведут
борьбу за два стратегических пункта. В распоряжении ![]() имеется
два полка, в распоряжении
имеется
два полка, в распоряжении ![]() три; обе
стороны должны распределить свои силы между двумя пунктами. В каждом пункте выигрыш
стороны, направившей в него
три; обе
стороны должны распределить свои силы между двумя пунктами. В каждом пункте выигрыш
стороны, направившей в него ![]() полков, против
стороны, направившей
полков, против
стороны, направившей ![]() полков, равен
полков, равен ![]() при
при ![]() нулю
при
нулю
при ![]() при
при ![]() Общий
выигрыш каждого противника равен сумме его выигрышей в двух пунктах.
Сформулировать задачу как игру двух лиц с нулевой суммой и найти решение
методом ЛП. У к а з а н и е.Пользуясь симметрией игры, можно привести к
двум переменным (и решить графически) каждую из задач ЛП в двойственной паре.
Общий
выигрыш каждого противника равен сумме его выигрышей в двух пунктах.
Сформулировать задачу как игру двух лиц с нулевой суммой и найти решение
методом ЛП. У к а з а н и е.Пользуясь симметрией игры, можно привести к
двум переменным (и решить графически) каждую из задач ЛП в двойственной паре.
Библиографический список
1. Линейное программироваине: Метод. указания /Сост.М.Н. Соколовский.- Омск: Изд-во ОмГТУ, 2003 – 36с.
2. Линейное программирование. Двойственность. Зависимость оптимальных планов от исходных данных: Метод указания /Сост. М.Н. Соколовский.- Омск: Изд-во ОмГТУ, 2003 -36 с.
3. Мулен Э. Теория игр (с примерами из математической экономики). – М.: Мир, 1985.
См. также библиографический список в [1].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.