Транспортная задача. Матричные игры: Методические указания к практическим занятиям, страница 12

Выбрав определенную стратегию  , игрок А получит выигрыш, равный одному из элементов  ой строки   матрицы   конкретное значение выигрыша зависит от неизвестного игроку А выбора стратегии (столбца матрицы)  игроком В. Игрок В не знает, какую стратегию выбрал А. Однако «осторожный» игрок А учитывает, что В мог каким-то образом догадаться  о сделанном им выборе    и ответить такой стратегией ,  для которой  наименьшее  из чисел   Число

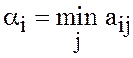                                                 (15)

называется  гарантированным выигрышем стратегии  Наибольшее значение гарантированного выигрыша,

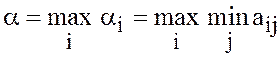                                      (16)

называется  нижней ценой игры  или максимином. Стратегия    с максимальным гарантированным выигрышем    (таких может быть несколько) называется максиминной. Эта стратегия является наилучшим выбором  с точки зрения «осторожного» игрока А и обеспечивает ему выигрыш  не меньше нижней цены  против  любой  стратегии игрока В.

Величины, связанные с осторожным поведением игрока В, определяются аналогично. Наибольший элемент го столбца матрицы

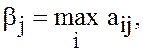                                                       (17)

называется гарантированным проигрышем стратегии  Наименьшее из чисел

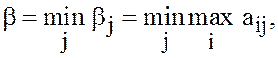                                              (18)

называется верхней ценой игры  или  минимаксом. Стратегия   с минимальным гарантированным проигрышем   называется минимаксной стратегией, эта стратегия обеспечивает игроку   проигрыш не больше верхней цены    против любой стратегии игрока А. Максиминная и минимаксная стратегии называются гарантирующими.

В любой игре нижняя цена не больше верхней,

                                                             (19)

Действительно, из определений гарантированных выигрышей (15) и гарантированных проигрышей (17) следует, что

                           (20)

Неравенство (19) получается из (20) при    где   и  максиминная и минимаксная  стратегии,  для которых    

Пример 8. (Антагонистическая конкуренция). Две фирмы А и В  производят  и реализуют сезонный товар, который пользуется спросом    дней. Цена единицы товара установлена антимонопольным законом  и не может быть использована в борьбе за рынок сбыта. Единственный инструмент каждой из фирм в этой борьбе – выбор момента поступления своего товара на рынок. Ежедневный спрос на товар равен  (единиц товара), не меняется в течении всего периода и может быть удовлетворён даже каждой фирмой в отдельности. Считается, что:  товар фирмы, которая вышла на рынок позже другой, имеет более высокое качество;  в любой день реализуется только товар более высокого качества;  при одновременном выходе фирм на рынок ежедневная реализация товара каждой из них составляет 50 % спроса. Цель  фирмы  А - максимизировать объём своих продаж за сезон, цель фирмы В - минимизировать объём продаж фирмы А («разорить» фирму А).

Составить матрицу игры, соответствующей описанной конфликтной ситуации при     и  найти гарантированные выигрыши и проигрыши, нижнюю и верхнюю цены,  гарантирующие стратегии.

Решение:Каждая фирма должна принять решение о дне начала продаж. Игрок (фирма) А имеет    стратегий (вариантов принятия решения) вида:

начать продажи с го дня сезона,  Cтратегии игрока В описываются аналогично: начать продажи с го дня сезона, 

Элемент   платёжной матрицы размера    равен объёму продаж товара фирмы А за весь сезон при условии, что  фирмы А и  В начали продажи с го  и го дня соответственно. При    в течение   дней, с го по ый  включительно, реализуется только товар фирмы А, в остальные дни товар фирмы А не продаётся и, следовательно,   При   продажи фирмы А равны  половине спроса за период с го   по ый день  и    а при  всему спросу за тот же период  и   Полученные формулы позволяют составить платёжную матрицу для любого  , в частности,

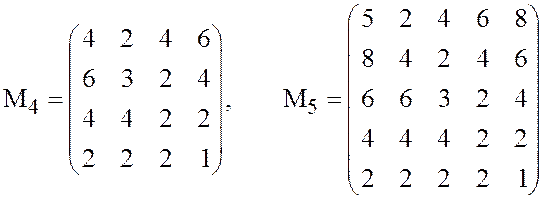
матрицы игры «антагонистическая конкуренция»  при     и    соответственно (выбор конкретного значения   не влияет  на исследование игры, в    и    принято ).