Транспортная задача. Матричные игры: Методические указания к практическим занятиям, страница 16

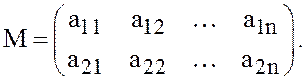
Выигрыши смешанных стратегий    игрока    против чистых стратегий противника находятся по формулам (26), в данном случае

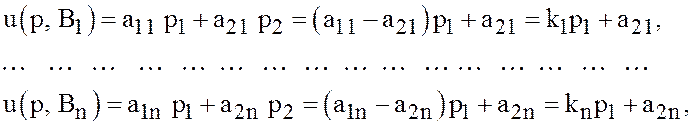
а гарантированный  выигрыш стратегии  по формуле (30),

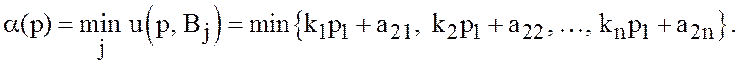
В декартовой системе координат с осями    и    графиком функции 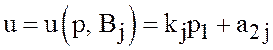  будет прямая, проходящая через точки      и    а графиком функции    нижняя огибающая  этих    прямых:  при любом  конкретном    точка     на графике    совпадает с самой нижней  из точек  прямых    с заданной абсциссой    Нетрудно понять, что нижняя огибающая представляет собой  выпуклую  вверх ломаную, звенья которой – отрезки некоторых из    рассматриваемых прямых. Наибольшая  из ординат точек ломаной   равна по определению (29)  нижней цене    а  абсцисса точки c ординатой    вероятности    в  максиминной  смешанной стратегии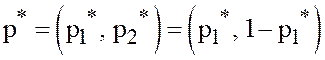 

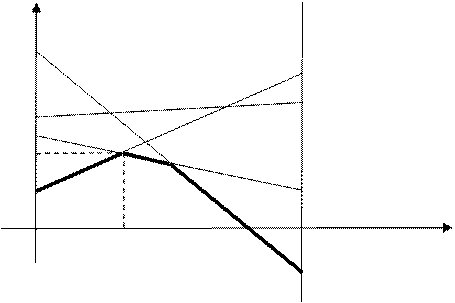
Рис.10

На рис.10 выпуклая ломаная    состоит из отрезков трех прямых, соответствующих  чистым стратегиям    прямые, соответствующие  остальным  расположены выше ломаной. Наибольшую ординату имеет точка    пересечения прямых, соответствующих     и   , поэтому нижнюю цену игры    и максиминную стратегию 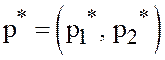   можно найти из системы уравнений

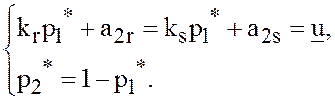                               (34)

Рассмотрим смешанную стратегию 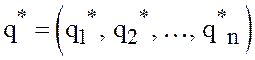 игрока , в которо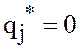й   при   а вероятности  и   удовлетворяют уравнениям

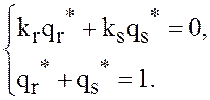                                        (35)

Здесь угловые коэффициенты    и     имеют разные знаки (смотри рис.10) и поэтому   (проверьте). Заметим, что уравнения двух прямых, проходящих через точку 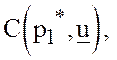    можно записать в виде

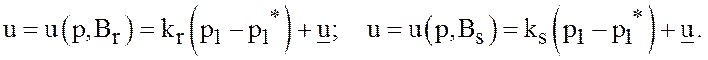
В первом из равенств (27) положим 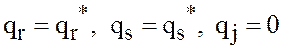 при   , в двух оставшихся ненулевых слагаемых заменим    и    на выражения этих величин из уравнений соответствующих прямых. В результате получим

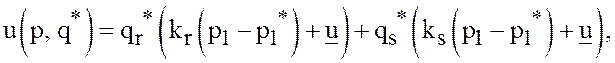
а после очевидных преобразований и учёта равенств (35)

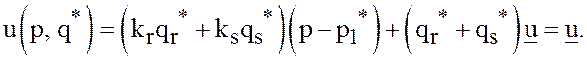
Равенство 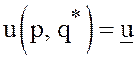   справедливо   для  любых   поэтому 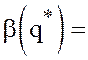 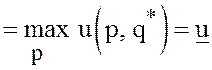    и 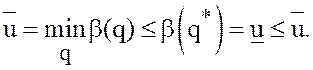    Из последней цепочки следует равенство    Таким образом игра   с графиком    представленным на рис.10, имеет решение 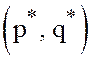   и цену   которые определяются из систем уравнений  (34) и (35). Аналогично  находится решение и цена любой игры  , для которой максимальную ординату на ломаной  имеет точка пересечения двух прямых с угловыми коэффициентами  разных знаков. Другие возможные случаи  расположения точек с максимальной  ординатой  на   ломаной     рассматриваются   в  упражнении 11.

Пример 10. Найти решение и цену игры с матрицей

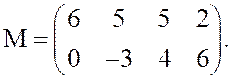
Решение. Игра не имеет решения в чистых стратегиях, т.к.  (проверьте). По матрице  М  находим  выигрыши 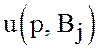   стратегии  

рис. 11(обратите внимание на то, как связаны с матрицей М ординаты точек пе-  ресечения прямых 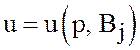   с осью  и вертикальной прямой  ).  По рис.11 определяем, что на ломаной    наибольшую ординату имеет точка С пересечения  прямых     и    с угловыми коэффициентами     и    Системы уравнений (34) и (35) в данном примере запишутся в виде:

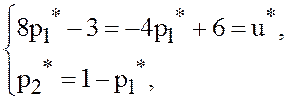
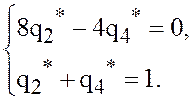
Решая обе системы, находим        Ответ:

Решение и цену игры с матрицей  размера    можно найти по графику зависимости гарантированного проигрыша     игрока    от вероятности    смешанной стратегии 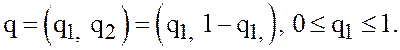  Этот график совпадает с верхней огибающей семейства прямых  ,

   и представляет собой  вогнутую  (выпуклую вниз) ломаную линию. Графическое решение конкретной игры   разбирается ниже в примере 11.