Транспортная задача. Матричные игры: Методические указания к практическим занятиям, страница 6

Умножим каждое уравнение системы (3) на  соответствующий потенциал     или     и просуммируем левые и правые части полученных уравнений. Результатом такого  суммирования будет уравнение 

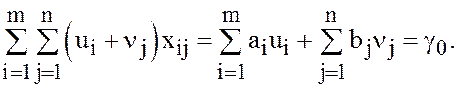
С учётом этого уравнения  выражение целевой  функции (2) можно записать в виде

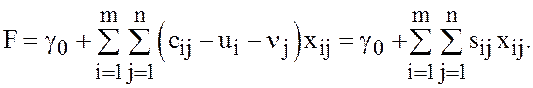                    (9)

Величины

                   (10)

называются  псевдостоимостями  клеток таблицы. По определению потенциалов (8)     для занятых клеток, и формула (9) даёт выражение  целевой функции любого допустимого плана через  свободные  (соответствующие  незанятым клеткам таблицы) переменные. Из единственности такого выражения следует, что   и псевдостоимости    не  зависят  от выбора значения   при вычислении потенциалов. Формула (9) позволяет сформулировать следующий

Признак оптимальности. Опорная таблица ТЗ, в которой все  псевдостоимости  неотрицательны,    представляет оптимальный  план ТЗ.

Действительно, пусть 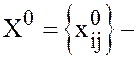 план, соответствующий такой таблице, 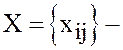произвольный  допустимый план. Тогда  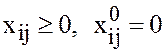 для всех незанятых клеток, и по формуле (9)  ,  т.е.

Пример 3. Вычислить потенциалы и псевдостоимости опорной таблицы на рис. 3г)  в примере 2. Проверить выполнение признака оптимальности.

Решение. Результаты всех вычислений представлены на рис.5: таблица 3г)  из примера 2 дополнена значениями потенциалов – числа слева от строк и над столбцами,  и  псевдостоимостей - числа  в левых нижних  углах незанятых клеток (цикл и метки  на рис.5 понадобятся нам позже, при разборе данного примера на них надо просто не обращать внимания).

по формуле (8):         Псевдостоимости находятся по формулам (10):    В данной таблице среди псевдостоимостей есть отрицательные – признак оптимальности не выполнен.  

Перестройка по циклу и метод потенциалов. В заданной опорной таблице ТЗ выберем незанятую клетку  По теореме 2 существует единственный содержащий эту клетку цикл     в котором все остальные клетки заняты. Перестройкой по циклу     называется преобразование исходной таблицы по следующим правилам:  

 В клетках  цикла    расставим  метки   или   так, чтобы     получила метку , а соседние  клетки цикла – метки разных знаков;  обозначим через     наименьшее  из чисел   записанных в клетках с меткой   .

           Выберем клетку    с меткой  , длякоторой   если  таких клеток несколько, выберем  одну (любую) из них.

 В клетку   запишем  число  становится занянятой;  в клетке   сотрем число   становится незанятой.

           В остальных клетках цикла заменим  на где знак перед  совпадает с меткой клетки; все клетки, не входящие в цикл   оставим без изменений.

При перестройке по правилам     сохраняются все свойства опорных таблиц ТЗ (см. а),  б),  в) на стр.7):

- неотрицательность всех «новых» следует из определения числа

- для любого ряда  таблицы  возможны изменения только в двух клетках, сосед- них по циклу   сумма  чисел ряда  при  этом  не меняется, т.е. сохраняется  свойство а);

- по правилу       становится занятой, а  - незанятой, поэтому число занятых клеток не меняется и сохраняется свойство б);