Транспортная задача. Матричные игры: Методические указания к практическим занятиям, страница 18

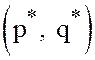Таким образом для игр с положительной  платёжной матрицей    доказана справедливость теоремы Неймана о минимаксе: чтобы найти решение  и  цену    такой  игры,  надо по матрице   составить пару двойственных задач ЛП (36-37)  и (38-39), найти оптимальные планы этих задач и вычислить вероятности 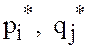   и цену   по формулам (40). Можно показать, что такой способ нахождения решения и цены игры применим к любой матричной игре, удовлетворяющей условию    Последнее требование заведомо выполнено, если   (см. (31));  неравенство  легко проверяется.

Если    прибавим ко всем элементам платёжной матрицы 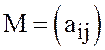      одно и тоже число   Обозначим через     и    платёжную функцию  и нижнюю цену в чистых стратегиях игры с матрицей 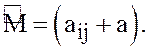   Тогда

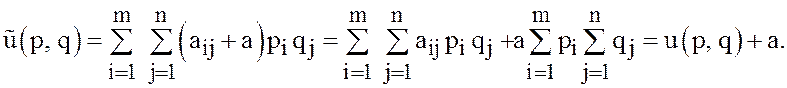
Очевидно, что   Каждое двойное неравенство в критерии седловой пары (33) для функции    эквивалентно  такому же неравенству для функции  постоянное слагаемое    сокращается. Это означает, что любое решение (седловая пара) 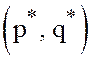   игры с матрицей    будет решением и в исходной игре с матрицей   Чтобы найти цену    исходной игры, надо отнять постоянную   от цены    игры с матрицей    

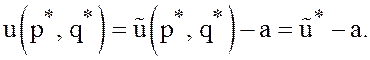
Пример 12. Найти решение и цену игры с матрицей   из примера 8. Описать оптимальное поведение  фирм   и    в рассматриваемой конфликтной ситуации.

Решение. В игре с матрицей    можно исключить сначала доминируемые стратегии    и    а затем стратегию   (после первого сокращения  ),

            

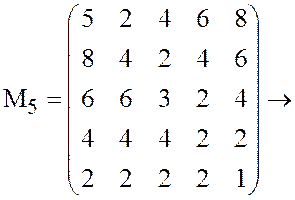
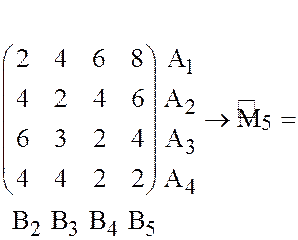
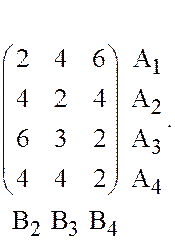
По матрице   (в ней все элементы положительны) составим задачу ЛП (36-37)  и  применим для её решения симплекс-метод  [1,стр.25].

16/3

 

6

13/8

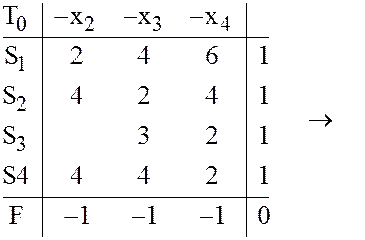
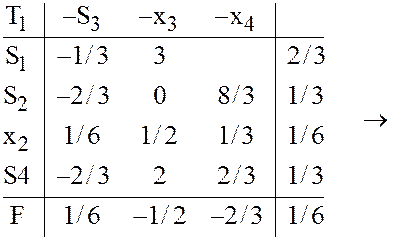
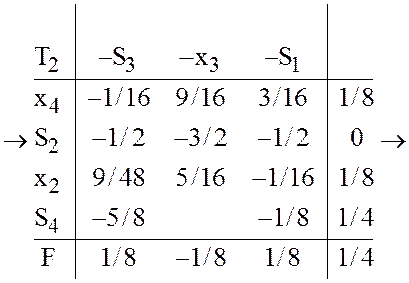
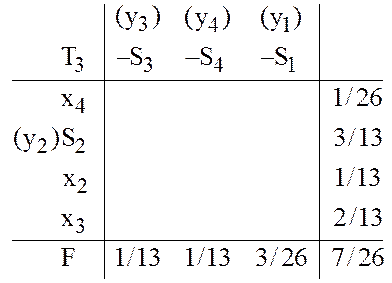
Здесь  балансовые переменные  [1, стр.7];  в начальной симплексной таблице   эти переменные  являются базисными. Отметим, что «внутренняя» часть   совпадает с матрицей   По заключительной таблице    находим (сравните с примером 6 из [1])  оптимальные значения переменных и целевых функций задач (36-37)  и  (38-39), соответствующих матрице   (в таблице   эта переменная двойственной задачи – свободная!),   

В решении исходной игры с матрицей      вероятности  доминируемых чистых стратегий равны нулю,    цена   и остальные вероятности вычисляются по формулам (40):      

  

  Окончательно  получаем                  

т.е.  при    фирма    должна начинать продажи  с 1-го, 3-го  или  4-го дня сезона с вероятностями     и     соответственно,  а  фирма  со 2-го, 3-го или  4-го дня с вероятностями    и 

Пример 13. Найти решение и цену игры с матрицей

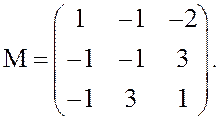
Решение. Игра не имеет решений в чистых стратегиях, т.к.   (проверьте). Матрица    размера   в данном примере не сокращается, т.к. в игре нет доминируемых чистых стратегий (сравните все  пары строк  и все пары столбцов матрицы). При    графический метод  не применим, решение (в смешанных стратегиях) будем искать с помощью приведения игры к задаче ЛП.

В отличие от примера 12, в котором    и, следовательно,   здесь  Поэтому ко всем элементам матрицы  надо прибавить число   такое, что    например    В результате получим матрицу

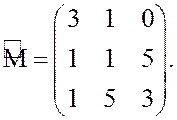
При переходе от   к    решение игры не меняется, цены двух игр  связаны равенством    По матрице    составим задачу ЛП (36-37)  и решим эту задачу симплекс-методом:

5

3

           

64/15

                                  

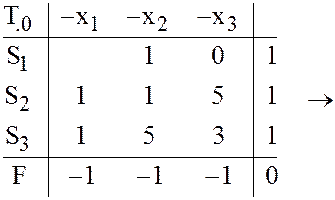
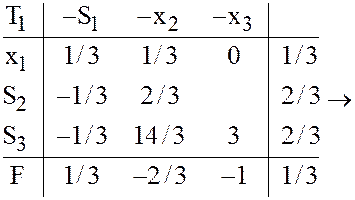
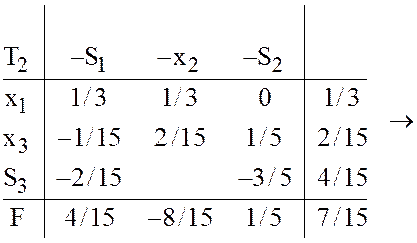
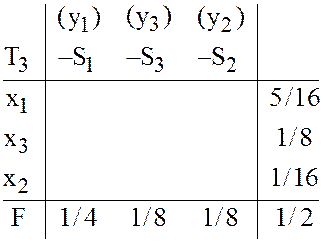
По заключительной таблице  находим:    Цена игры 

и вероятности 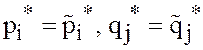 вычисляются по формулам (40):

           

Ответ:

У п р а ж н  е н и я

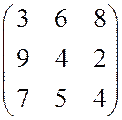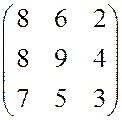8. Для следующих платёжных матриц определить верхнюю и нижнюю цены в чистых стратегиях и гарантирующие чистые стратегии игроков а)            б)               в)   .

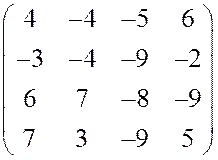Найти седловые элементы матриц (если такие существуют) и соответствующие решения в чистых стратегиях.