В
некоторых случаях можно уменьшить размеры матрицы исследуемой игры за счет
исключения заведомо невыгодных чистых стратегий. Говорят, что (чистая)
стратегия ![]() игрока
игрока ![]() доминируется
стратегией
доминируется
стратегией ![]() и пишут
и пишут ![]() если
все элементы
если
все элементы ![]() ой строки матрицы
игры не больше соответствующих элементов
ой строки матрицы
игры не больше соответствующих элементов ![]() ой
строки,
ой
строки, ![]() Стратегия
Стратегия ![]() игрока
игрока
![]() доминируется стратегией
доминируется стратегией ![]() (обозначение:
(обозначение: ![]() ), если все элементы
), если все элементы ![]() ого
столбца не меньше соответствующих элементов
ого
столбца не меньше соответствующих элементов ![]() ого
столбца,
ого
столбца, ![]()
По
определению, замена чистой стратегии ![]() на
на ![]() не уменьшает выигрыш игрока
не уменьшает выигрыш игрока ![]() , а замена
, а замена ![]() на
на ![]() не увеличивает проигрыш игрока
не увеличивает проигрыш игрока ![]() при любых ответах противника, если
при любых ответах противника, если ![]() или
или ![]() соответственно.
Используя это свойство, можно показать, что при исследовании игры, в которой
есть доминируемые стратегии, надо просто «сократить» платёжную матрицу,
вычеркнув из неё строки и столбцы, соответствующие доминируемым стратегиям.
Цена исходной игры
соответственно.
Используя это свойство, можно показать, что при исследовании игры, в которой
есть доминируемые стратегии, надо просто «сократить» платёжную матрицу,
вычеркнув из неё строки и столбцы, соответствующие доминируемым стратегиям.
Цена исходной игры ![]() равна цене игры с сокращенной
матрицей; в решении
равна цене игры с сокращенной
матрицей; в решении 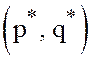 исходной игры
вероятности доминируемых стратегий равны нулю, а все остальные
совпадают с соответствующими вероятностями «сокращенной» игры.
исходной игры
вероятности доминируемых стратегий равны нулю, а все остальные
совпадают с соответствующими вероятностями «сокращенной» игры.
Пример
11. Найти решение и цену игры с матрицей ![]() из
примера 8. Описать оптимальное поведение фирм
из
примера 8. Описать оптимальное поведение фирм ![]() и
и ![]() в рассматриваемой конфликтной ситуации.
в рассматриваемой конфликтной ситуации.
Решение:Игра не
имеет решения в чистых стратегиях, т.к. ![]() (см.
пример 8). По матрице
(см.
пример 8). По матрице ![]() находим
находим ![]()
![]() и
и ![]() , т.е.
, т.е. ![]()
и ![]() доминируемые стратегии (в данном случае
это следует также из
доминируемые стратегии (в данном случае
это следует также из ![]() и
и ![]() Вычеркнув
из
Вычеркнув
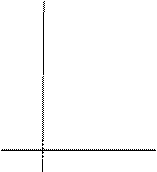
из ![]() 4-ю строку и 1-ый столбец, получим
матрицу, в которой можно вычеркнуть столбец, соответствующий
4-ю строку и 1-ый столбец, получим
матрицу, в которой можно вычеркнуть столбец, соответствующий ![]() ( в «сокращенной» игре
( в «сокращенной» игре ![]() ),
),
![]()
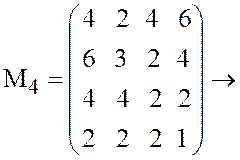
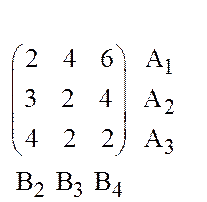
На
рис.12 представлена геометрическая интерпретация игры с матрицей ![]()
4 4 3 C
2 1/2 1 Рис.12 |
Здесь
Верхняя огибающая
|
По
рис. 12 находим (сравните с примером 10) сначала ![]()
![]() из уравнений
из уравнений ![]()
![]()
![]() а затем
а затем ![]()
![]() из уравнений
из уравнений ![]()
![]() (
(![]() и
и ![]() угловые коэффициенты прямых
угловые коэффициенты прямых ![]() и
и ![]() пересекающихся
в точке С). Все остальные вероятности
пересекающихся
в точке С). Все остальные вероятности ![]() и
и ![]() в решении
в решении 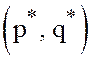 равны
нулю. Таким образом, в игре с матрицей
равны
нулю. Таким образом, в игре с матрицей ![]()
![]()
т.е. в примере 8 при ![]() фирма
фирма ![]() должна
с вероятностями
должна
с вероятностями ![]()
начинать
продажу с 1-го или 3-го дня сезона, а фирма ![]() с
вероятностями
с
вероятностями ![]() со 2-го или 3-го дня сезона.
со 2-го или 3-го дня сезона.
Приведение
матричной игры к задаче ЛП. Покажем сначала, как сводится к задаче ЛП игра, в
которой все элементы ![]() платёжной матрицы
платёжной матрицы ![]() положительны. Рассмотрим задачу ЛП
положительны. Рассмотрим задачу ЛП
![]() (36)
(36)
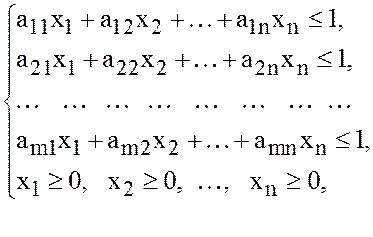 (37)
(37)
и двойственную к ней задачу [2, cтр. 3]
![]() (38)
(38)
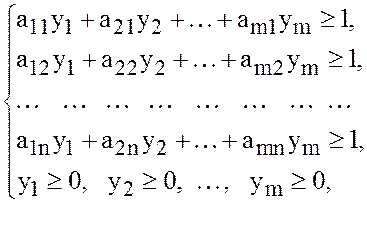 (39)
(39)
Обе задачи имеют допустимые планы:
ограничениям (37) удовлетворяют планы вида ![]() при достаточно
малых
при достаточно
малых ![]() а ограничениям (39) – планы вида
а ограничениям (39) – планы вида ![]() при достаточно больших
при достаточно больших ![]() По первой теореме двойственности [2,
стр.4] обе задачи разрешимы, т.е. имеют оптимальные планы
По первой теореме двойственности [2,
стр.4] обе задачи разрешимы, т.е. имеют оптимальные планы 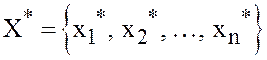 и
и
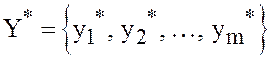 соответственно, причём
экстремальные значения
соответственно, причём
экстремальные значения ![]() и
и ![]() целевых функций совпадают,
целевых функций совпадают,
![]()
(неравенство
![]() следуют из допустимости планов
следуют из допустимости планов ![]()
![]() Положим
Положим
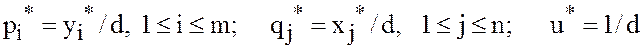 (40)
(40)
и покажем,
что смешанные стратегии 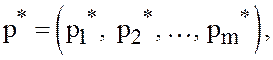
![]()
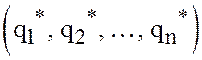 образуют седловую
пару (решение) игры с матрицей
образуют седловую
пару (решение) игры с матрицей
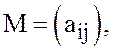 а
а ![]() цена
этой игры.
цена
этой игры.
Подставим
 в ограничения (37) и (39) и разделим все
неравенства на
в ограничения (37) и (39) и разделим все
неравенства на ![]() В результате получим систему
неравенств.
В результате получим систему
неравенств.
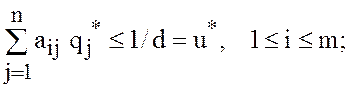
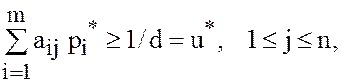
которую с учётом (25) и (26) можно записать в виде
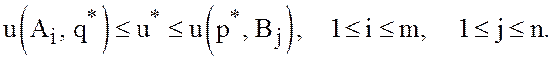 (41)
(41)
Из второй теоремы двойственности [2, стр. 4] следует (проверьте!), что
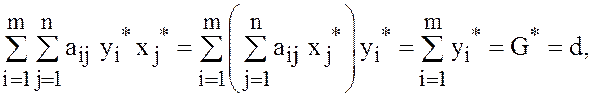
и поэтому
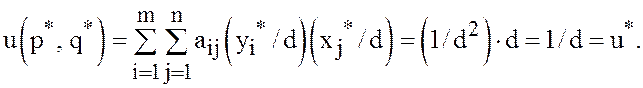
Из
равенства 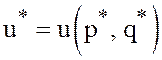 и (41) следует, что пара
и (41) следует, что пара 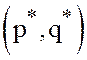 удовлетворяет системе неравенств (33),
т.е. является седловой. Напомним, что
удовлетворяет системе неравенств (33),
т.е. является седловой. Напомним, что ![]()
![]() для любой седловой пары
для любой седловой пары ![]() (см.
абзац после формулы (33)). Поэтому совпадение числа
(см.
абзац после формулы (33)). Поэтому совпадение числа ![]() из (40) с
из (40) с 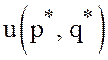 означает, что
означает, что ![]() цена игры.
цена игры.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.