Транспортная задача. Матричные игры: Методические указания к практическим занятиям, страница 13

По матрице   последовательно находим гарантированные выигрыши (минимальные элементы строк)    нижнюю цену игры    и  максиминные стратегии   и  (для этих стратегий    Аналогично определяются гарантированные  проигрыши (максимальные элементы столбцов)    верхняя цена игры   и минимаксные стратегии   и  (для этих стратегий ).Для игры с матрицей   имеем:   максиминные стратегии;  единственная минимаксная стратегия.

Отметим, что справедливое для всех конечных игр соотношение (19) в данном примере выполнено как строгое неравенство 

          Пример 9. Найти гарантированные выигрыши и проигрыши, нижнюю и верхнюю цены, гарантирующие стратегии игры с матрицей

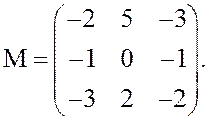
Решение.Вычисление гарантированных выигрышей и проигрышей обычно оформляется следующим образом: рядом с каждой строкой (столбцом) платёжной матрицы справа (снизу) записывается наименьший (наибольший) элемент этой строки (столбца). В рассматриваемом примере получится таблица

-1

-1

-1

                                                        

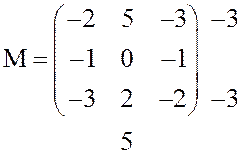
Выделяя в «дополнительном» столбце (строке) наибольшее (наименьшее) число, находим нижнюю цену     и  верхнюю цену   в данном случае соотношение (19) реализуется в виде равенства  Максиминной стратегией   будет    а  минимаксными     и   

В конечной игре максиминная стратегия гарантирует игроку   выигрыш не меньше нижней цены  В то же время   не может рассчитывать на выигрыш больше  верхней цены   т.к.   может выбрать одну из своих минимаксных стратегий и проиграть (дать выиграть игроку )  не больше   Аналогичное рассуждение показывает, что игрок  , имея возможность проиграть не больше   не может рассчитывать на проигрыш меньше   Для игры, в которой     это означает, что гарантирующие  стратегии дают игрокам результаты, которые невозможно улучшить, и, следовательно, соответствуют их

оптимальному  поведению. Очевидно, что в этом случае выбор любой пары   гарантирующих стратегий выгоден обоим игрокам.

При   нет таких убедительных причин считать гарантирующие стратегии «неулучшаемыми», как это было в случае   и при выборе оптимального поведения надо использовать другие соображения. Рассмотрим для определенности игру с матрицей    из примера 8 и возможные рассуждения игроков в этой игре. Предположим, что игрок   собирается применить одну из своих гарантирующих (максиминных) стратегий     или   для которых    Считая, что противник также планирует выбор своей (единственной) гарантирующей стратегии    он выберет, конечно,    или    так  как  максимальные элементы 3-го столбца в матрице   Игрок   может повторить эти рассуждения игрока   отказаться от стратегии   и применить  наилучший ответ при условии, что   выбрал     или   (сравните пары чисел из 1-ой и 4-ой строки в  столбцах матрицы ) и т.д. Понятно, что в любой игре, для которой  подобные рассуждения можно продолжать бесконечно – окончательное решение о выборе стратегии так и не будет принято.

Учитывая всё вышеизложенное, введём следующие определения:если в конечной игре   то общее значение   этих величин называется ценой игры, гарантирующие  стратегии игроков называются оптимальными, а любая пара 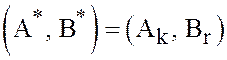  таких стратегий – решением игры;если

 то говорят, что конечная игра  не имеет решения.

В соответствии с принятыми определениями игры из примера 8 не имеют решения    а игра из примера 9 имеет цену    и два решения,    и 

По  определению игра имеет решение тогда и только тогда, когда   Чтобы проверить это равенство, достаточно вычислить    и    по формулам (16) и (18). Другая форма критерия существования решения связана с понятием седловой точки.

Элемент   платёжной матрицы    называется седловым, если он является одновременно наименьшим в своей строке и наибольшим в своем столбце, т.е. удовлетворяет неравенствам

                                                              (21)

или, что то же самое,  двойному равенству

                                           (22)