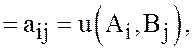Транспортная задача. Матричные игры: Методические указания к практическим занятиям, страница 15

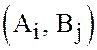 т.е. паре   в конечной    игре и паре 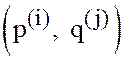   в её смешанном  расширении соответствует один и тот же результат. Это означает, что чистые стратегии можно считать частными случаями смешанных, а игру в чистых стратегиях – частным случаем игры в смешанных стратегиях; для конечных игр и их смешанных расширений принято общее название матричные игры. Будем называть чистыми не только стратегии исходной игры, но и соответствующие им смешанные стратегии, а вместо   и    писать просто    и    В этих обозначениях замена   на   в формуле (24) запишется в виде

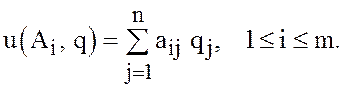                          (25)

Аналогично получаем

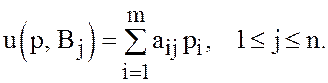                                (26)

Величины     и 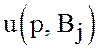   представляет собой средние выигрыши игрока  (проигрыши игрока ) в случаях, когда один из игроков применяет чистую стратегию. Нетрудно проверить, что значения платёжной функции (24) в общем случае выражаются через эти величины по формулам

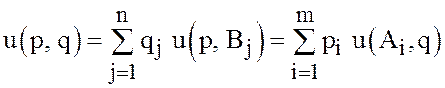.               (27)

Определения основных понятий, связанных с игрой в смешанных стратегиях, повторяют все определения для конечных игр. Величины

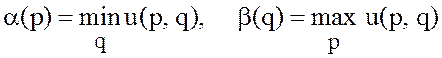                    (28)

называются гарантированным выигрышем стратегии    и  гарантированным проигрышем стратегии    а числа

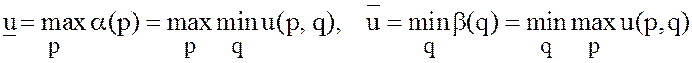      (29)

нижней ценой и верхней ценой игры в смешанных стратегиях. Стратегия  (стратегия ) называется максиминной (минимаксной), если  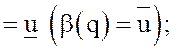  максиминные и минимаксные стратегии называются гарантирующими.

Замечание. Все глобальные экстремумы в определениях (28), (29) существуют по известному свойству функций, непрерывных на замкнутом ограниченном множестве; в любой матричной игре существует хотя бы одна максиминная и хотя бы одна минимаксная смешанная стратегия.

В дальнейшем будет использоваться следующее свойство платёжной функции   экстремумы  в (28) достигаются уже на чистых стратегиях, т.е.   и    можно вычислять по формулам

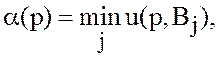
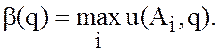                     (30)

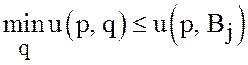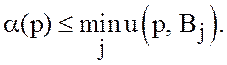Действительно, частный случай смешанной стратегии  , поэтому при любых  и, следовательно  В то же время из (27) и равенства     следует, что

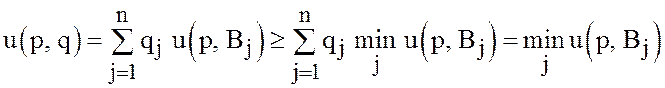
при любых     и   , поэтому 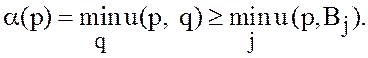 Таким образом   не больше и не меньше, чем 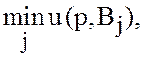  т.е. верно первое равенство в (30); второе равенство доказывается аналогично.

В любой матричной игре выполнены неравенства

                                                       (31)

Здесь    доказывается аналогично (19) для чистых стратегий, а крайние неравенства получаются из определения чисел    с помощью (30). Например,

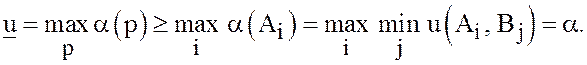
В этой цепочке  последовательно используются: определение числа    то, что чистые стратегии – частные случаи смешанных; первое  из равенств (30) при   равенство 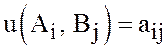    и определение числа

Пара смешанных стратегий 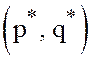   называется   седловой   или  реше-

нием матричной игры, если для любых    и    выполнены неравенства

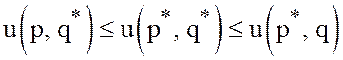                            (32)

(сравните с определением (21) и теоремой о седловой точке игры в чистых  стратегиях). Отметим сразу, что  бесконечная совокупность неравенств (32) эквивалентна своей конечной части, состоящей из всех неравенств, для которых   и   - чистые стратегии, т.е. системе 

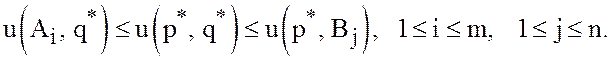             (33)

Доказательство эквивалентности (32) и  (33) предоставляется читателю (используйте формулы (27)).

Седловая пара смешанных стратегий существует тогда и только тогда, когда    компонентами седловой пары могут быть только гарантирующие стратегии; из  следует, что любая пара гарантирующих смешанных стратегий является седловой и при этом проверка всех этих утверждений аналогична доказательству теоремы о седловой точке в чистых стратегиях. Седловая пара 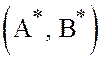   чистых стратегий является, очевидно, решением матричной игры. Однако такие чистые пары существуют не в любой игре (только при  ). Основная теорема теории матричных игр – теорема Джона фон Неймана о минимакcе – утверждает, что   т.е. для любой матричной игры существует решение 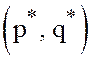  в смешанных стратегиях и цена игры 

Для произвольной платёжной матрицы нахождение решения (седловой пары) 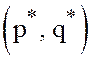    и цены    сводится к задаче ЛП. Матричные игры, в которых один из игроков имеет только две чистые стратегии, просто решаются графическим методом.

Графическое решение игр    и   При    матрица игры имеет вид