Транспортная задача. Матричные игры: Методические указания к практическим занятиям, страница 7

- если в некотором цикле   есть отличная от  незанятая клетка исход- ной таблицы, то эта клетка будет незанятой и в новой  таблице; если     

единственная  незанятая клетка исходной таблицы в   , то по теореме 2 цикл

 совпадает с   и незанятой клеткой новой таблицы в   будет   в любом случае при перестройке сохраняется свойство в).

Таким образом, результатом перестройки по циклу всегда будет новая опорная таблица ТЗ.

Пусть 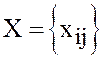   и 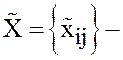 опорные планы, соответствующие исходной и перестроенной таблицам. Сравним    и  , вычисляя  оба значения целевой функции по формуле  (9) с псевдостоимостями    и свободным членом  исходной таблицы. Напомним, что в занятых клетках исходной таблицы  В незанятых клетках исходной таблицы равны  0 все числа   и  кроме   (проверьте!). Подставляя эти значения    в (9), получим    и, следовательно,

                                   (11)

Если план   не оптимальный, выберем клетку   для которой  (см. признак оптимальности). Число    всегда неотрицательно,   причем   возможно только для вырожденного плана  При   по формуле (11)    т.е. перестройка по циклу  улучшает  план исходной таблицы. В случае   исходная  и перестроенная таблицы отличаются только расположением занятых нулями клеток и представляют один и тот же (вырожденный) план.

При решении ТЗ методом потенциалов строится  та же самая  последовательность улучшающихся планов, которая получилась бы  при применении симплекс-метода. Однако вычисления, связанные с перестройкой  по циклу, гораздо проще, чем  соответствующий пересчет симплексных таблиц.

Алгоритм  метода  потенциалов

Шаг 1. Построить начальную опорную таблицу ТЗ методом СЗУ или методом МС, объявить полученную таблицу и соответствующий опорный план текущими.

Шаг 2. (Проверка оптимальности). В текущей таблице вычислить потенциалы и псевдостоимости.

а) если все псевдостоимости неотрицательны, то текущий план-оптимальный; если все  псевдостоимости незанятых клеток  положительны (нет равных нулю), то оптимальный план – единственный.

б) если среди псевдостоимостей есть отрицательные, выбрать клетку   с максимальной по модулю отрицательной  псевдостоимостью  (любую, если таких несколько) и построить цикл , в котором - единственная  незанятая клетка.

Шаг 3 (Улучшение плана). Текущую таблицу перестроить по циклу , объявить  полученную таблицу и соответствующий опорный план текущими.

Шаг 4. Перейти к шагу 2.

Пример 4.  Найти оптимальный план ТЗ из примера 1 методом потенциалов.

Решение:Примем  за  начальную таблицу, построенную  методом СЗУ

в  примере 2, рис.3г). Потенциалы и псевдостоимости этой таблицы вычислены в примере 3, рис.5. Среди псевдостоимостей    есть отрицательные, из них максимальной по модулю является   Цикл   с единственной незанятой клеткой    и метки    и    в его вершинах изображены на рис. 5. Выполним перестройку по циклу . Для этого вычислим   и выберем одну из клеток , с меткой , для которой  например, клетку  (1, 1). Далее запишем   в клетку  (3, 1),  сотрем   в клетке  (1, 1) и пересчитаем значения    в  остальных  клетках из