Числовые и функциональные ряды: Конспект лекций (Геометрическая прогрессия. Экстремальное свойство сумм Фурье)

Министерство образования и науки РФ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Омский государственный технический университет»

Н.И. Николаева

РЯДЫ

Конспект лекций

Часть 6

Омск

Издательство ОмГТУ

2012

УДК

ББК

Рецензенты:

Ю.Ф.Стругов, д-р физ.-мат. наук;

С.Е.Макаров, канд. физ.-мат. наук, доцент

Николаева Н.И.

Ряды. Часть 6 / Н.И. Николаева. – Омск: Изд-во ОмГТУ, 2012. –   с.

Пособие представляет собой конспект лекций, читаемых автором  на втором  курсе технического университета, и предназначено для студентов всех форм обучения. Часть 6 является заключительной и  включает в себя два  раздела: «Числовые ряды» и  «Функциональные ряды». Изложение сопровождается              достаточным количеством примеров, поясняющих наиболее важные теоретические положения, иллюстрирующих  теоретический материал и дающих образцы решения задач.

Автор также выражает признательность А. Лымарю и зав. методическим кабинетом кафедры Царицинской Т.Г. за большую помощь в техническом оформлении рукописи.

Печатается по решению редакционно-издательского совета

Омского государственного технического университета

Оглавление

Глава 13.  РЯДЫ

13.1. Числовые ряды

Неверно трактовать ряд как «сумму бесконечного числа слагаемых», так как он является не обычной суммой, для которой справедливы знакомые по элементарной математике законы действий такие как, например, коммутативность, а новым  понятием, которое необходимо правильно истолковать. Некритическое применение привычных правил в действиях с рядами может привести                        к ложным результатам.

Пронаблюдаем основные понятия теории рядов на частном, достаточно простом и известном примере.

13.1.1. ГЕОМЕТРИЧЕСКАЯ  ПРОГРЕССИЯ

Последовательность вида  называется геометрической прогрессией;  называется первым членом прогрессии (будем считать, что ),  – ее знаменателем,  – -м, или общим членом.

ПРИМЕРЫ. 

а) 6, 12, 24, 48, 96;  б) 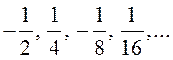 – числовые геометрические прогрессии;

в)  г) 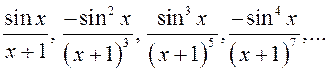 – функциональные геометрические прогрессии.

Если в геометрической прогрессии конечное число членов (примеры а)                   и в)), то она называется конечной и ее сумма легко находится. Если же прогрессия содержит бесконечное число членов (примеры б) и г)), то она называется бесконечной.

Выведем формулу для вычисления суммы конечной геометрической прогрессии:

.

Умножим это равенство на  и вычтем одно из другого:

.

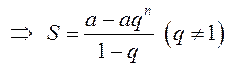Если прогрессия бесконечна, то прежде чем говорить о сумме всех  ее членов, надо условиться, какой смысл придавать этому выражению.

Рассмотрим сумму  первых  членов бесконечной геометрической прогрессии, которую будем называть ее -й частичной суммой:

.

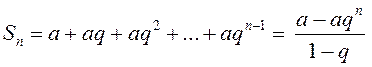
Естественно считать суммой  всех членов бесконечной прогрессии  предел последовательности ее частичных сумм:  . Из определения предела последовательности следует (см.гл.4), что чем больше слагаемых в частичной сумме вида , тем ближе она к своему  предельному значению.