Таким
образом, о сумме можно говорить лишь тогда, когда существует конечный
![]() . В этом случае бесконечная
геометрическая прогрессия называется сходящейся. Если этот предел не
существует или бесконечен, то будем называть прогрессию
расходящейся.
. В этом случае бесконечная
геометрическая прогрессия называется сходящейся. Если этот предел не
существует или бесконечен, то будем называть прогрессию
расходящейся.
Итак,
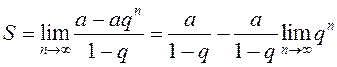 .
.
1. Пусть ![]() . В этом случае прогрессия называется бесконечно
убывающей, она сходится, а ее сумма
. В этом случае прогрессия называется бесконечно
убывающей, она сходится, а ее сумма
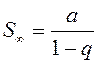 .
(13.1)
.
(13.1)
Для такой
прогрессии ![]() с точностью
с точностью 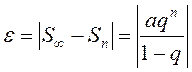 .
.
2. Пусть ![]() . В этом случае геометрическая прогрессия расходится
и суммы не имеет.
. В этом случае геометрическая прогрессия расходится
и суммы не имеет.
3. Если ![]() , то
, то ![]() .
.
4. Если ![]() , то суммы с четными номерами
, то суммы с четными номерами ![]() , а с нечетными –
, а с нечетными – ![]() .
Это означает, что
.
Это означает, что ![]() не существует.
не существует.
В обоих случаях прогрессия расходится.
Таким
образом, бесконечная геометрическая прогрессия сходится, если является
бесконечно убывающей, то есть при ![]() . Если
. Если ![]() , то геометрическая прогрессия расходится
и суммы не имеет.
, то геометрическая прогрессия расходится
и суммы не имеет.
13.1.2. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ.
СВОЙСТВА ЧИСЛОВЫХ РЯДОВ
Рассмотрим последовательность действительных чисел ![]() .
.
ОПРЕДЕЛЕНИЕ. Числовым рядом называется выражение
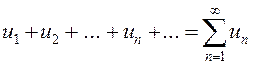 ,
,
![]() называется первым членом ряда,
называется первым членом ряда, ![]() –
– ![]() -м, или общим
членом.
-м, или общим
членом.
Ряд считается заданным, если задан его общий член.
ОПРЕДЕЛЕНИЕ. Сумма ![]() первых слагаемых ряда
называется его
первых слагаемых ряда
называется его ![]() -й частичной суммой:
-й частичной суммой: 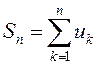 .
.
ПРИМЕРЫ.
а)
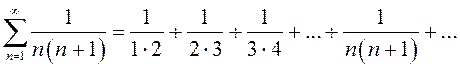 ;
;
б)
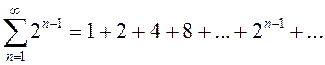 ;
;
в)
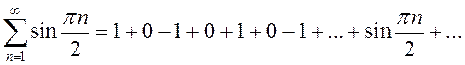 .
.
Рассмотрим последовательности частичных сумм этих рядов:
а)
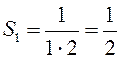 . Заметим, что
. Заметим, что 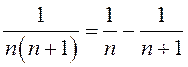 ,
поэтому
,
поэтому
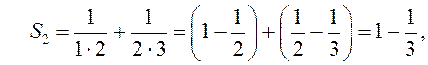
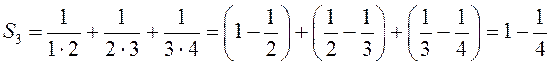 ,
,
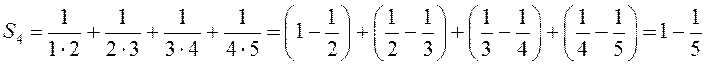 , …,
, …,
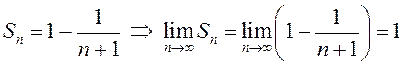 .
.
Естественно
считать, что 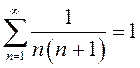 .
.
б)
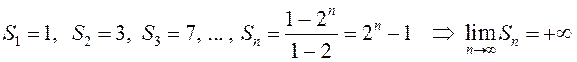 , поэтому сумма ряда
, поэтому сумма ряда 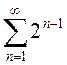 не существует.
не существует.
в)
![]() не существует, значит, ряд
не существует, значит, ряд 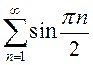 суммы не имеет.
суммы не имеет.
ОПРЕДЕЛЕНИЕ. Числовой ряд называется сходящимся, если существует
конечный предел ![]() последовательности его частичных
сумм
последовательности его частичных
сумм ![]() . Этот предел называется суммой сходящегося
ряда:
. Этот предел называется суммой сходящегося
ряда: ![]() .
.
Если![]() не существует или бесконечен,
то ряд называется расходящимся.
не существует или бесконечен,
то ряд называется расходящимся.
Если ряд
сходится, то ![]() называется
называется ![]() -м остатком сходящегося ряда.
-м остатком сходящегося ряда.
Рассмотрим некоторые свойства числовых рядов.
1.
Если ряды  и
и 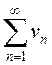 сходятся,
то сходится и ряд
сходятся,
то сходится и ряд
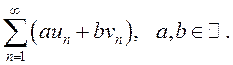
ДОКАЗАТЕЛЬСТВО.
Обозначим 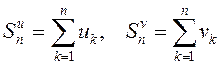 .
.
По условию
существуют конечные пределы ![]() и
и ![]() . Тогда
. Тогда 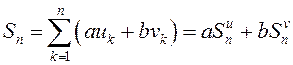 ,
отсюда
,
отсюда ![]() . Это по определению означает, что ряд
. Это по определению означает, что ряд 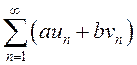 сходится.
сходится.
ЗАМЕЧАНИЕ.
Из сходимости ряда 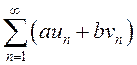 не следует сходимость
не следует сходимость  и
и 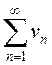 .
.
ПРИМЕР.
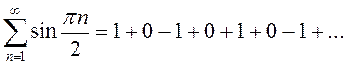 расходится, также расходится и ряд
расходится, также расходится и ряд 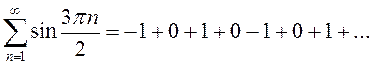 . Но сумма этих рядов равна нулю,
то есть
. Но сумма этих рядов равна нулю,
то есть 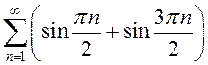 сходится.
сходится.
2.
Если ряд  сходится, то сходится любой ряд,
полученный из данного отбрасыванием или дописыванием любого конечного
числа слагаемых.
сходится, то сходится любой ряд,
полученный из данного отбрасыванием или дописыванием любого конечного
числа слагаемых.
ДОКАЗАТЕЛЬСТВО.
Пусть отброшено ![]() слагаемых, сумма которых равна
слагаемых, сумма которых равна ![]() . Найдется частичная сумма
. Найдется частичная сумма ![]() данного ряда, в которой содержатся все отброшенные
слагаемые (во всех суммах с большими номерами они тоже содержатся).
Поэтому
данного ряда, в которой содержатся все отброшенные
слагаемые (во всех суммах с большими номерами они тоже содержатся).
Поэтому ![]() и
и ![]() , где
, где ![]() – сумма исходного ряда. Это по определению
означает, что ряд, полученный после отбрасывания
– сумма исходного ряда. Это по определению
означает, что ряд, полученный после отбрасывания ![]() его
членов, сходится.
его
членов, сходится.
Случай дописывания конечного числа членов ряда доказывается аналогично.
Из доказательства этого свойства следует, что его можно переформулировать следующим образом: произвольное изменение конечного числа членов ряда не влияет на его поведение, то есть сходящийся ряд остается сходящимся, а расходящийся – расходящимся.
13.1.3. НЕОБХОДИМЫЙ ПРИЗНАК СХОДИМОСТИ РЯДА
Не всегда можно точно найти сумму сходящегося ряда, как это было сделано,
например, для ряда 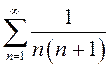 . Однако, если быть уверенным в
том, что рассматриваемый ряд сходится, можно найти его сумму приближенно со
сколь угодно большой точностью, так как
. Однако, если быть уверенным в
том, что рассматриваемый ряд сходится, можно найти его сумму приближенно со
сколь угодно большой точностью, так как ![]() , где
, где ![]() – частичная сумма ряда с
достаточно большим номером. Для этого рассмотрим теоремы, которые называются признаками
сходимости числовых рядов. Они позволяют установить факт сходимости (или
расходимости) ряда не по определению, а с помощью более простых и технологичных
приемов.
– частичная сумма ряда с
достаточно большим номером. Для этого рассмотрим теоремы, которые называются признаками
сходимости числовых рядов. Они позволяют установить факт сходимости (или
расходимости) ряда не по определению, а с помощью более простых и технологичных
приемов.
ТЕОРЕМА (необходимый признак сходимости числового ряда)
Если ряд  сходится, то его общий член стремится к
нулю:
сходится, то его общий член стремится к
нулю: ![]() .
.
ДОКАЗАТЕЛЬСТВО. Так как ряд  сходится,
то по определению существует
сходится,
то по определению существует ![]() , где
, где ![]() – частичная сумма ряда.
– частичная сумма ряда.
При ![]() число
число![]() также
неограниченно растет, поэтому
также
неограниченно растет, поэтому ![]() . Отсюда
. Отсюда ![]() , но
, но 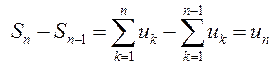 .
Следовательно,
.
Следовательно, ![]() .
.
ЗАМЕЧАНИЕ.
Из теоремы следует, что если ![]() , то
, то  расходится.
расходится.
ПРИМЕР.
Исследовать на сходимость ряд 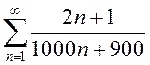 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.