Числовые и функциональные ряды: Конспект лекций (Геометрическая прогрессия. Экстремальное свойство сумм Фурье), страница 13

        ЗАМЕЧАНИЕ. Для -периодической функции  коэффициенты Фурье находятся по формулам (13.30), (13.34) и (13.35). Но из свойств определенного интеграла от периодической функции (см.п.8.5) следует, что отрезок интегрирования при вычислении коэффициентов ряда можно произвольно сдвигать, если это удобно, не изменяя его длины:

.

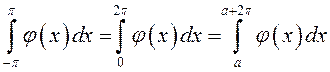13.2.7. РЯД  ФУРЬЕ  ДЛЯ ФУНКЦИЙ С  ПЕРИОДОМ  

Пусть  – -периодическая функция, удовлетворяющая условиям                 Дирихле на отрезке . По определению периода . Введем новую переменную  по формуле 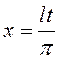 и покажем, что относительно  рассматриваемая функция будет -периодической.

Действительно,  .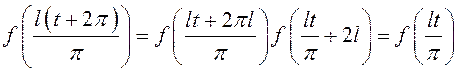

Следовательно,  можно разложить в ряд Фурье на отрезке :

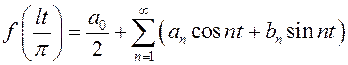                     ,                           (13.36)

где         .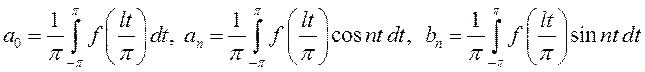

Возвратимся теперь к старой переменной : 

.

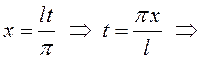
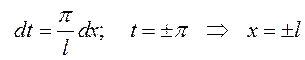Тогда имеем:

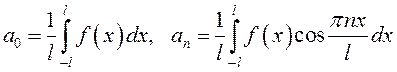               ,                      (13.37)

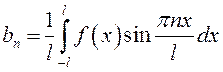                               .                                     (13.38)

Равенство (13.36) можно переписать:

                 ,                       (13.39)

где коэффициенты  вычисляются по формулам (13.37), (13.38).

Это и есть ряд Фурье для -периодической функции.

        ПРИМЕР. Разложить в ряд Фурье функцию 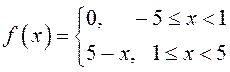.                              Найти сумму ряда в точках .

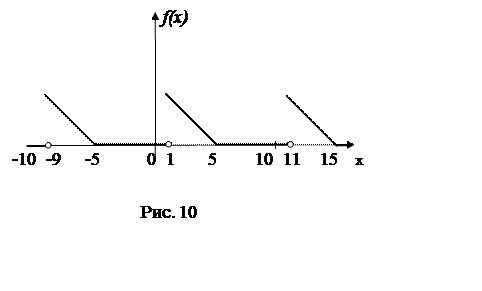
График этой функции представлен на рис.10. Ее период .

                                          

Чтобы найти сумму ряда в указанных точках, воспользуемся теоремой Дирихле. Заметим, что сделать это можно, не вычисляя коэффициентов ряда и, соответственно, не зная его общего члена.

Точки  и  являются точками непрерывности заданной периодической функции (рис.10), поэтому

; .

Точка  является точкой разрыва (рис.10), поэтому по теореме Дирихле

.

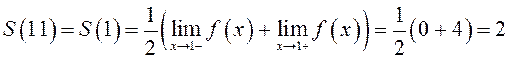Найдем теперь коэффициенты Фурье данной функции.

.

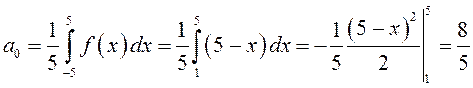При вычислении  применим формулу интегрирования по частям (см.п.7.4):   

;

.

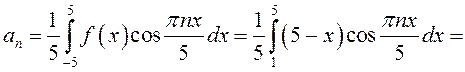
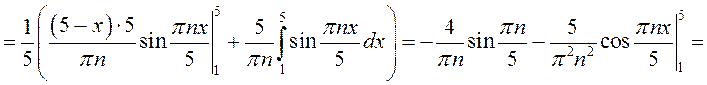
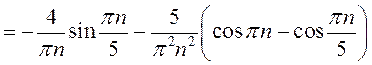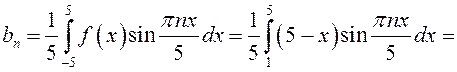
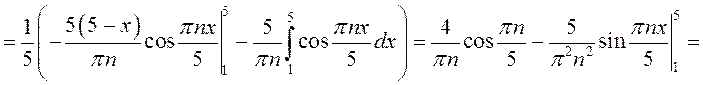
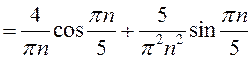Таким образом, разложение заданной функции в ряд Фурье имеет вид:

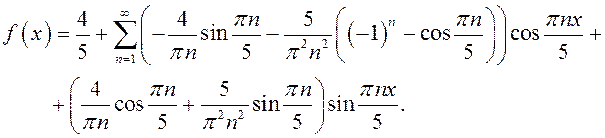
13.2.8. РЯД  ФУРЬЕ  ДЛЯ  ЧЕТНЫХ  И  НЕЧЕТНЫХ  ФУНКЦИЙ

Пусть  – четная -периодическая функция, удовлетворяющая условиям Дирихле на отрезке . Тогда 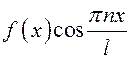 – четная, а  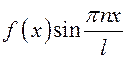– нечетная функции. Поэтому в соответствии со свойствами определенного интеграла по симметричному отрезку (см.п.8.5) имеем:

,

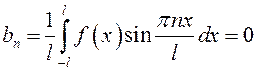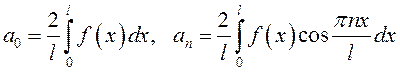.                  (13.40)

Таким образом, четная функция представляется  рядом Фурье вида 

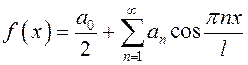, коэффициенты которого вычисляются по формулам (13.40).

Аналогично, если  – нечетная -периодическая функция, то 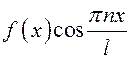 – нечетная, а  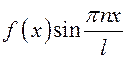– четная функции. Отсюда , а

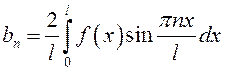                                   ,                                  (13.41)

и ряд Фурье такой функции содержит только нечетные синусы:

.

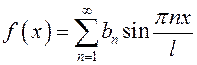Коэффициенты этого ряда находятся по формуле (13.41).

13.2.9. РАЗЛОЖЕНИЕ  В  РЯД  ФУРЬЕ

НЕПЕРИОДИЧЕСКИХ ФУНКЦИЙ

При решении различных прикладных задач возникает необходимость               разложения в ряд Фурье непериодических функций.

Пусть функция  определенная лишь для всех , удовлетворяет               условиям Дирихле на этом отрезке. Чтобы разложить ее в ряд Фурье, построим периодическое продолжение  на всю числовую прямую, то есть найдем функцию , удовлетворяющую таким условиям:

1. = ,

2. ,

3.  удовлетворяет условиям Дирихле на любом отрезке оси .

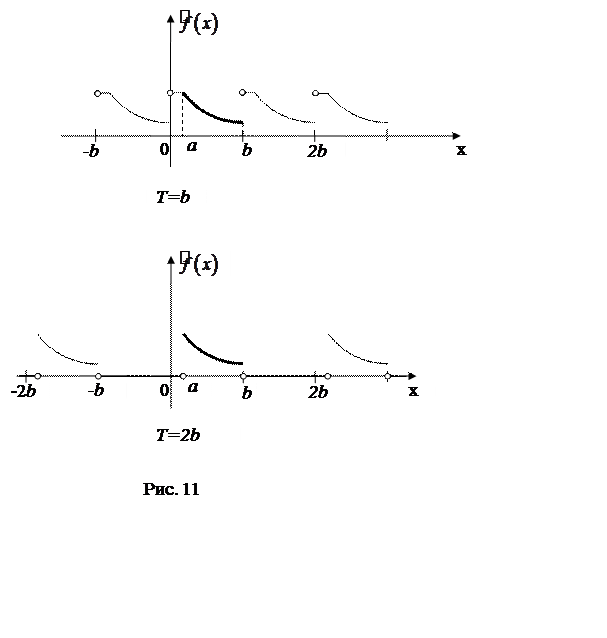
Понятно, что таких функций существует бесконечно много: при их                      построении может меняться и величина периода , и способ определения функции в пределах одного периода (рис.11).

 

Продолжив таким образом  разложим периодическую функцию                     в ряд Фурье.  Так как реально заданной является лишь часть этой  функции  при , то полученное разложение будем рассматривать только в точках этого отрезка. При этом во всех точках , где  непрерывна, согласно теореме Дирихле сумма ряда . В точках разрыва первого рода функции , принадлежащих ,

.

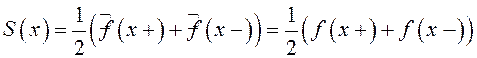Значения  и  будут зависеть от способа продолжения функции                          за пределы отрезка .

Предположим теперь, что функция  задана на отрезке . Чтобы разложить ее в ряд Фурье на этом отрезке, продолжим эту функцию сначала                на отрезок , а затем построим периодическое продолжение  с периодом . Очевидно, получившийся ряд для  будет зависеть от того, как именно доопределена  на промежутке . Сделать это можно различными способами. Рассмотрим два из них.