Исследовать на сходимость – значит, ответить на вопрос: данный ряд сходится или расходится?
Найдем предел
общего члена ряда: 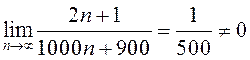 . Так как этот предел отличен от
нуля, то ряд расходится по необходимому признаку.
. Так как этот предел отличен от
нуля, то ряд расходится по необходимому признаку.
ЗАМЕЧАНИЕ.
Необходимый признак сходимости достаточным не является, то есть из того,
что ![]() , нельзя заключить, что ряд
, нельзя заключить, что ряд  сходится: в этом случае он может как
сходиться, так и расходиться.
сходится: в этом случае он может как
сходиться, так и расходиться.
ПРИМЕР.
Рассмотрим ряд 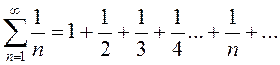 . Числовой ряд такого
вида называется гармоническим рядом.
. Числовой ряд такого
вида называется гармоническим рядом.
Заметим, что его
общий член стремится к нулю: 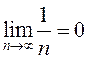 . Покажем, что, тем не
менее, гармонический ряд расходится.
. Покажем, что, тем не
менее, гармонический ряд расходится.
Сгруппируем слагаемые гармонического ряда таким образом:
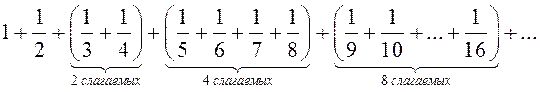
и построим вспомогательный ряд:
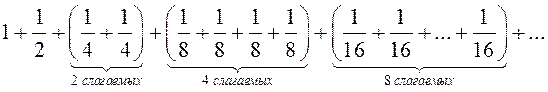 .
.
Обозначим
частичную сумму гармонического ряда ![]() , а
, а ![]() – частичную сумму вспомогательного ряда.
Тогда
– частичную сумму вспомогательного ряда.
Тогда
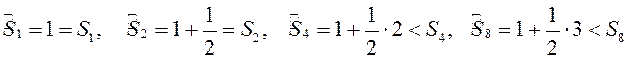 ,
,
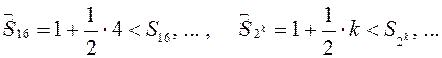 .
.
По теореме о предельном переходе в неравенствах (см.гл.4)
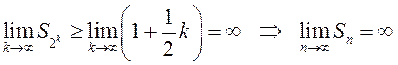 .
.
Следовательно,
гармонический ряд расходится. Вычисляя его частичные суммы,
можно увидеть, что он расходится очень медленно: к примеру, ![]() , а
, а ![]() .
.
13.1.4. ДОСТАТОЧНЫЕ ПРИЗНАКИ СХОДИМОСТИ
ЗНАКОПОЛОЖИТЕЛЬНЫХ ЧИСЛОВЫХ РЯДОВ
Рассмотрим
числовой ряд  , все члены которого
положительны. Такой ряд будем называть знакоположительным.
, все члены которого
положительны. Такой ряд будем называть знакоположительным.
Так как ![]() , то
, то ![]() , то
есть последовательность
, то
есть последовательность ![]() его частичных сумм возрастает.
его частичных сумм возрастает.
В таком случае возможны два варианта (см.гл.4):
а) если
![]() неограниченно растет, то
неограниченно растет, то ![]() , значит, ряд расходится;
, значит, ряд расходится;
б) если
![]() возрастает и остается ограниченной сверху,
то существует конечный
возрастает и остается ограниченной сверху,
то существует конечный ![]() и ряд сходится.
и ряд сходится.
Таким
образом, для доказательства сходимости знакоположительного ряда достаточно
доказать ограниченность сверху последовательности ![]() его
частичных сумм.
его
частичных сумм.
ТЕОРЕМА
(первый признак сравнения сходимости знакоположительных рядов). Пусть  и
и 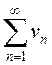 –
знакоположительные ряды. Если, начиная с
некоторого номера,
–
знакоположительные ряды. Если, начиная с
некоторого номера, ![]() и ряд
и ряд 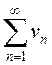 сходится,
то сходится и ряд
сходится,
то сходится и ряд  .
.
ДОКАЗАТЕЛЬСТВО.
Так как изменение конечного числа членов ряда не влияет на его сходимость, то
будем считать, что неравенство ![]() выполняется
выполняется ![]() .
.
Обозначим 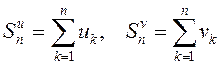 – частичные суммы данных рядов. Очевидно,
что
– частичные суммы данных рядов. Очевидно,
что ![]() , кроме того, так как
, кроме того, так как 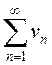 – знакоположительный ряд, то
– знакоположительный ряд, то ![]() возрастает. Этот ряд по условию сходится,
поэтому существует
возрастает. Этот ряд по условию сходится,
поэтому существует ![]() , причем
, причем ![]() .
.
Таким образом, ![]() , то есть
, то есть ![]() ограничена
сверху, поэтому
ограничена
сверху, поэтому  сходится. Что и требовалось
доказать.
сходится. Что и требовалось
доказать.
ТЕОРЕМА
(второй признак сравнения сходимости знакоположительных рядов). Пусть  и
и 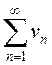 –
знакоположительные ряды. Если, начиная с
некоторого номера,
–
знакоположительные ряды. Если, начиная с
некоторого номера, ![]() и ряд
и ряд 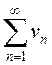 расходится,
то расходится и ряд
расходится,
то расходится и ряд  .
.
ДОКАЗАТЕЛЬСТВО.
Отбросим члены данных рядов, для которых неравенство ![]() неверно.
неверно.
Так как 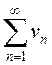 – расходящийся знакоположительный ряд, то
– расходящийся знакоположительный ряд, то ![]() ,
, 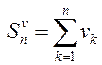 .
Отсюда
.
Отсюда ![]() , то есть
, то есть ![]() ,
, 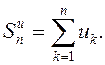 Это означает, что ряд
Это означает, что ряд  расходится.
расходится.
ПРИМЕР.
Исследовать сходимость рядов: а) 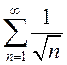 ; б)
; б) 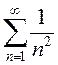 .
.
а)
Обозначим 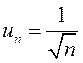 . В качестве ряда для сравнения выберем гармонический
ряд
. В качестве ряда для сравнения выберем гармонический
ряд 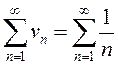 . Он расходится и
. Он расходится и 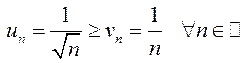 .
Значит, по второму признаку сравнения
.
Значит, по второму признаку сравнения 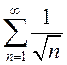 также расходится.
также расходится.
б) Обозначив
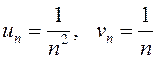 , получим, что
, получим, что ![]() . Но больший
ряд
. Но больший
ряд 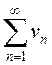 расходится, а потому сделать вывод о
поведении меньшего ряда
расходится, а потому сделать вывод о
поведении меньшего ряда  нельзя.
нельзя.
Попробуем
найти другой ряд для сравнения: пусть 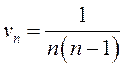 . Этот
ряд, как было показано в п.13.1.2, сходится и в таком случае
. Этот
ряд, как было показано в п.13.1.2, сходится и в таком случае
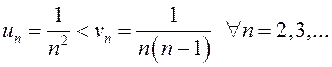 .
.
Следовательно, 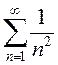 сходится по первому признаку сравнения.
сходится по первому признаку сравнения.
Рассмотренные примеры показывают, что правильный выбор ряда для сравнения требует опыта и интуиции. Более простым в этом смысле является предельный признак сравнения сходимости.
ТЕОРЕМА
(предельный признак сравнения сходимости знакоположительных рядов).
Пусть  и
и 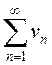 –
знакоположительные ряды. Если существует конечный
–
знакоположительные ряды. Если существует конечный 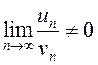 , то оба ряда сходятся или расходятся одновременно.
, то оба ряда сходятся или расходятся одновременно.
ДОКАЗАТЕЛЬСТВО.
По условию 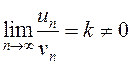 , причем очевидно, что
, причем очевидно, что ![]() . По определению предела
последовательности (см.гл.4)
. По определению предела
последовательности (см.гл.4)
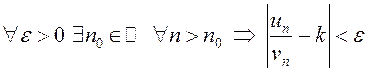 , или
, или
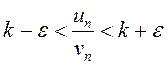 . (13.2)
. (13.2)
1) Пусть
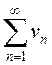 сходится, тогда, так как
сходится, тогда, так как ![]() , из неравенства (13.2) имеем:
, из неравенства (13.2) имеем:
![]() . Ряд
. Ряд 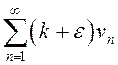 также
сходится по свойству 1, отсюда
также
сходится по свойству 1, отсюда  сходится по первому
признаку сравнения.
сходится по первому
признаку сравнения.
2) Пусть
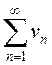 расходится, тогда
расходится, тогда 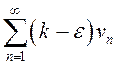 также
расходится. Выберем
также
расходится. Выберем ![]() так, что
так, что ![]() .
Из (13.2) имеем:
.
Из (13.2) имеем: ![]() . Следовательно,
. Следовательно,  расходится по второму признаку сравнения.
расходится по второму признаку сравнения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.