Числовые и функциональные ряды: Конспект лекций (Геометрическая прогрессия. Экстремальное свойство сумм Фурье), страница 7

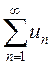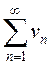        ТЕОРЕМА (об оценке остатка знакоположительного ряда). Пусть                   знакоположительные ряды  и  сходятся и . Тогда , где  – -й остаток первого ряда, а  – -й остаток второго ряда.

Без доказательства.

        ПРИМЕР. Найти приближенно сумму ряда 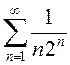 с точностью .

Для общего члена данного ряда справедлива, например, такая  оценка:

.

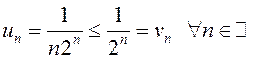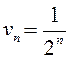 – общий член ряда геометрической прогрессии со знаменателем 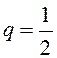, сумма которой находится по формуле (13.1): 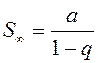. Тогда

.

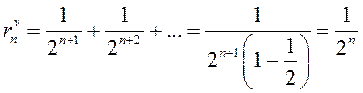Решая неравенство , находим, что , потому что . Так как  , то , поэтому можно утверждать, что для данного ряда  с точностью .

        ПРИМЕР. Оценить точность приближения  для ряда .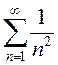

Оценим общий член данного ряда таким образом:

.

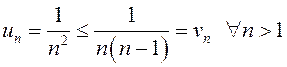Остаточный член вспомогательного ряда (см. п. 13.1.2)

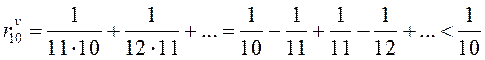, потому . Следовательно,  с точностью .

        ЗАМЕЧАНИЕ. Сравнивая результаты, полученные в рассмотренных примерах, можно сделать вывод, что 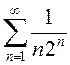  сходится гораздо быстрее ряда 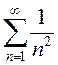: для достижения заданной точности в первом случае необходимо взять меньше членов ряда, чем во втором.

        ТЕОРЕМА (об оценке остатка знакопеременного ряда). Пусть знакопеременный ряд 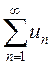 сходится абсолютно. Тогда модуль его -го остатка                       не превосходит -го остатка ряда, составленного из модулей его членов:

.

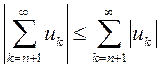Без доказательства.

        ПРИМЕР. Найти сумму ряда 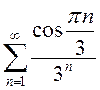  с точностью  .

Данный ряд является знакопеременным  и   .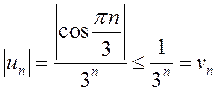

 – общий член ряда геометрической прогрессии со знаменателем 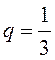, поэтому  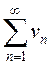сходится. Значит,  данный ряд  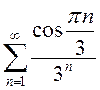сходится абсолютно.

Воспользуемся формулой (13.1):

.

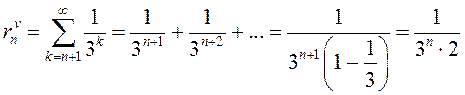Решая неравенство 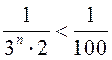, находим, что . Поэтому можно утверждать, что для исходного ряда  с точностью .

        ТЕОРЕМА (об оценке ряда, сходящегося по признаку Лейбница). Пусть ряд  сходится по признаку Лейбница. Тогда ,                      или модуль -го остатка ряда не превосходит модуля первого отброшенного слагаемого.

Утверждение этой теоремы следует из признака Лейбница.

        ПРИМЕР. Найти сумму условно сходящегося ряда 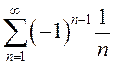 с точностью  .

Данный ряд является знакочередующимся. Он сходится по признаку Лейбница и 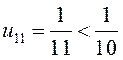 , поэтому  с заданной точностью .

        ПРИМЕР.  Найти сумму ряда 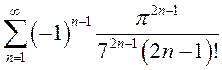 с точностью  .

Данный ряд также  является знакочередующимся. Легко проверить, применив                                к ряду  признак Даламбера, что он сходится абсолютно.  Найдем первый член ряда, модуль которого окажется меньше, чем 0,001:

;       .

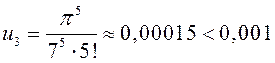По теореме об оценке остатка знакочередующегося ряда , значит, .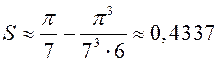

Далее будет показано, что сумма данного ряда равна 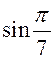,  поэтому                      в этом примере найдено приближенное значение 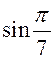 0,4337 с точностью .

13.2. Функциональные   ряды

13.2.1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ

Рассмотрим последовательность функций

, определенных .

        ОПРЕДЕЛЕНИЕ.  Функциональным рядом называется выражение

 называется первым членом функционального ряда,  – его -м, или                          общим членом.

Функциональный ряд считается заданным, если задан его общий член.

        ПРИМЕРЫ.

а)  ;

б) ;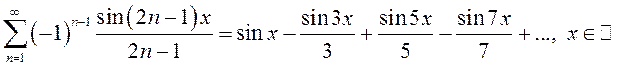

в)  ;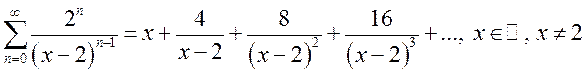

При фиксированном значении  функциональный ряд 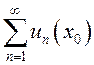                    становится числовым рядом – сходящимся или расходящимся.

        ПРИМЕРЫ. При  ряд а) становится сходящимся  числовым рядом 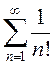,  ряд в) – расходящимся рядом .

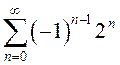При 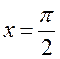 ряд б)  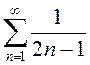 расходится, а при  сходится, так как ,  и сумма ряда в этом случае равна нулю.

        ОПРЕДЕЛЕНИЕ.  Если числовой ряд 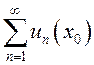   сходится, то точка  называется точкой сходимости функционального ряда .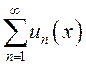

Совокупность всех точек сходимости функционального ряда называется его           областью сходимости.

Будем обозначать область сходимости функционального ряда .

Частичная сумма 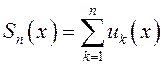 является функцией, определенной . Если же , то по определению суммы числового ряда существует конечный  .

        ОПРЕДЕЛЕНИЕ. Функция , определенная ,                     называется суммой функционального ряда.

Если , то  называется -м остатком функционального ряда.  Остаток функционального ряда так же, как и его сумма, является функцией, определенной на области сходимости.

        ПРИМЕР.   Найти область сходимости и сумму функционального ряда .

Ряд 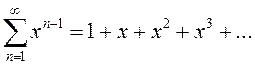 является рядом геометрической прогрессии со знаменателем , поэтому он сходится, если  (см.п.13.1.1).