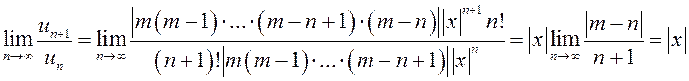 , так как
, так как ![]() при достаточно больших
при достаточно больших ![]() , а
, а  (см.гл.4).
(см.гл.4).
Отсюда
полученный ряд сходится, когда ![]() , то есть
, то есть ![]() .
.
Можно доказать,
что остаточный член (13.25) при таких ![]() стремится
к нулю, если
стремится
к нулю, если ![]() .
.
Таким образом,
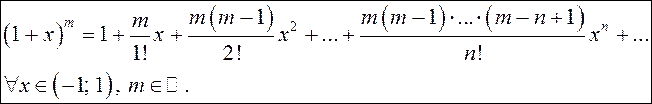 (13.26)
(13.26)
Функция ![]() называется биномом, поэтому
полученный ряд (13.26) называется биномиальным.
называется биномом, поэтому
полученный ряд (13.26) называется биномиальным.
При
натуральных значениях ![]() разложение будет конечным. В частности,
при
разложение будет конечным. В частности,
при ![]() можно получить известные формулы
сокращенного умножения:
можно получить известные формулы
сокращенного умножения:
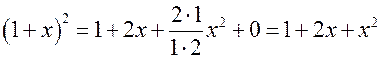 ;
;
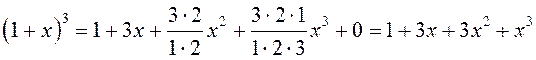 .
.
8. ![]() .
.
Так как 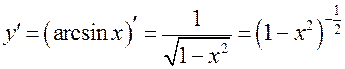 , то разложение в ряд Маклорена функции
, то разложение в ряд Маклорена функции ![]() можно получить, используя биномиальный ряд
(13.26).
можно получить, используя биномиальный ряд
(13.26).
Обозначим
![]() и напишем биномиальный ряд для
и напишем биномиальный ряд для  :
:
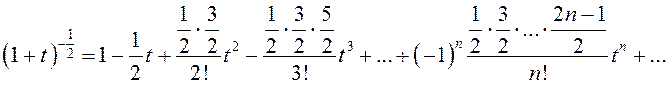 .
.
Упростим это
выражение. Во-первых, заметим, что ![]()
![]() . Во-вторых, воспользуемся обозначениями
. Во-вторых, воспользуемся обозначениями
![]() – произведение всех четных чисел от
2 до
– произведение всех четных чисел от
2 до ![]() – и
– и ![]() –
произведение всех нечетных чисел от 1 до
–
произведение всех нечетных чисел от 1 до ![]() .
.
Теперь имеем:
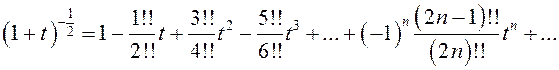 , отсюда
, отсюда
 .
.
Так как 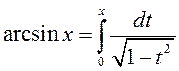 , то, проинтегрировав полученный ряд почленно
на интервале сходимости, получим:
, то, проинтегрировав полученный ряд почленно
на интервале сходимости, получим:
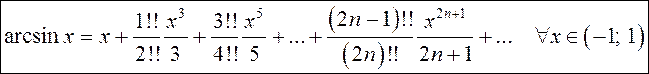 .
.
13.2.6. ТРИГОНОМЕТРИЧЕСКИЕ РЯДЫ ФУРЬЕ
Разложение функций в ряды Тейлора и Маклорена, кроме несомненных достоинств, обладает и рядом недостатков. К их числу относится то обстоятельство, что суммами сходящихся степенных рядов могут быть лишь бесконечно дифференцируемые функции. Однако в математике и ее приложениях приходится исследовать не только недифференцируемые функции, но и функции, имеющие «скачки», то есть разрывы первого рода.
Кроме
того, многие процессы в физике и технике являются периодическими (например,
переменный ток) и потому описываются периодическими функциями, характеризуемыми
равенством ![]() , где
, где ![]() период.
период.
Простейшими
периодическими функциями являются ![]()
![]() ,
,
![]() с наименьшим периодом
с наименьшим периодом 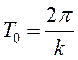 (коэффициент
(коэффициент ![]() называется
частотой) и
называется
частотой) и ![]() , для которой любое действительное число
является периодом. Из таких простых функций могут быть
составлены и более сложные, причем при их составлении необходимо использовать
синусоидальные величины разных частот. Например, функция
, для которой любое действительное число
является периодом. Из таких простых функций могут быть
составлены и более сложные, причем при их составлении необходимо использовать
синусоидальные величины разных частот. Например, функция 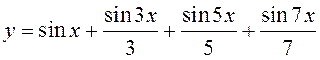 является периодической с
наименьшим периодом
является периодической с
наименьшим периодом ![]() , однако она существенно отличается
от функций, из которых составлена.
, однако она существенно отличается
от функций, из которых составлена.
Поставим
вопрос: можно ли данную периодическую функцию ![]() с
периодом
с
периодом ![]() представить в виде суммы конечного или
хотя бы бесконечного числа простейших периодических функций?
представить в виде суммы конечного или
хотя бы бесконечного числа простейших периодических функций?
ОПРЕДЕЛЕНИЕ. Функциональный ряд вида
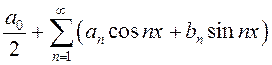 (13.27)
(13.27)
называется тригонометрическим
рядом. Постоянные числа ![]() называются коэффициентами
тригонометрического ряда.
называются коэффициентами
тригонометрического ряда.
Если ряд (13.27)
сходится, то его сумма является ![]() -периодической функцией
-периодической функцией ![]() .
.
Пусть ![]() -периодическая функция
-периодическая функция ![]() является суммой тригонометрического ряда
(13.27):
является суммой тригонометрического ряда
(13.27):
 . (13.28)
. (13.28)
Предположим, что
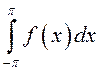 существует и равен сумме интегралов от членов
ряда в правой части равенства (13.28).
существует и равен сумме интегралов от членов
ряда в правой части равенства (13.28).
Чтобы найти коэффициенты этого ряда, проинтегрируем обе части (13.28):
 .
.
Так как
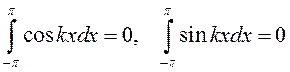 , (13.29)
, (13.29)
а 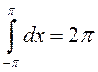 , то
, то 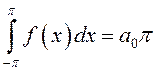 ,
откуда
,
откуда
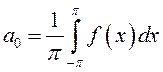 . (13.30)
. (13.30)
Для вычисления остальных коэффициентов нам потребуются следующие интегралы (см. п.8.5):
 , (13.31)
, (13.31)
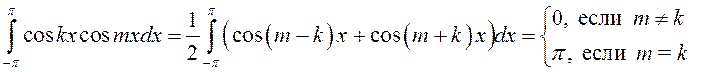 , (13.32)
, (13.32)
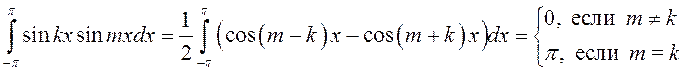 . (13.33)
. (13.33)
ОПРЕДЕЛЕНИЕ.
Функции ![]() и
и ![]() называются
ортогональными на отрезке
называются
ортогональными на отрезке ![]() , если
, если  .
.
Равенства
(13.29), (13.31) – (13.33) означают, что система функций ![]() является ортогональной на отрезке
является ортогональной на отрезке ![]() , так как функции этой системы попарно
ортогональны. Поэтому представление функции
, так как функции этой системы попарно
ортогональны. Поэтому представление функции ![]() в виде
ряда (13.28) можно назвать разложением ее по системе ортогональных на
отрезке
в виде
ряда (13.28) можно назвать разложением ее по системе ортогональных на
отрезке ![]() функций.
функций.
Чтобы
найти коэффициент ![]() , умножим обе части равенства
(13.28) на
, умножим обе части равенства
(13.28) на ![]() и проинтегрируем на отрезке
и проинтегрируем на отрезке ![]() , предполагая, что это возможно сделать:
, предполагая, что это возможно сделать:
 .
.
Тогда в соответствии с (13.29), (13.31) и (13.32), получим:
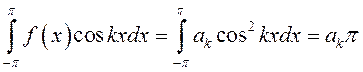 , откуда
, откуда
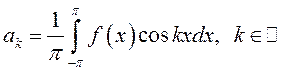 .
(13.34)
.
(13.34)
Аналогично,
умножая обе части (13.28) на ![]() и интегрируя на
и интегрируя на ![]() , с учетом (13.29),
(13.31) и (13.33) найдем, что
, с учетом (13.29),
(13.31) и (13.33) найдем, что
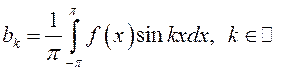 .
(13.35)
.
(13.35)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.