ЗАМЕЧАНИЕ. Функции, для которых формальный ряд Тейлора
составить можно, но он ни при каких значениях ![]() , кроме
, кроме ![]() , к ним не сходится, существуют.
, к ним не сходится, существуют.
Примером такой
функции является 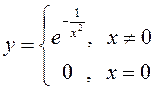 (рис. 4).
(рис. 4).
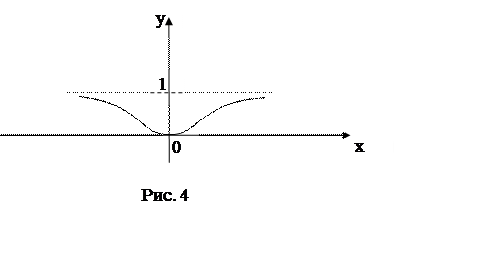 |
Можно показать
(с помощью довольно трудоемких вычислений), что ![]() ,
поэтому ряд Тейлора для этой функции в окрестности точки
,
поэтому ряд Тейлора для этой функции в окрестности точки ![]() имеет вид:
имеет вид: ![]() . Сумма
этого ряда равна нулю
. Сумма
этого ряда равна нулю ![]() , то есть формальный ряд
сходится, но не к той функции, для которой он составлен.
, то есть формальный ряд
сходится, но не к той функции, для которой он составлен.
Остаточный
член ряда Тейлора ![]() , очевидно, сам является рядом.
Однако он может быть представлен и в конечном виде. Например, можно
доказать, что между
, очевидно, сам является рядом.
Однако он может быть представлен и в конечном виде. Например, можно
доказать, что между ![]() и
и ![]() существует
точка
существует
точка ![]() такая, что
такая, что
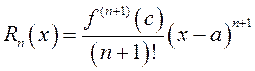 . (13.15)
. (13.15)
(13.15) называется остаточным членом ряда Тейлора в форме Лагранжа.
13.2.5. РАЗЛОЖЕНИЕ ОСНОВНЫХ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
В РЯД МАКЛОРЕНА
Если
положить ![]() , то ряд Тейлора для функции
, то ряд Тейлора для функции ![]() примет вид:
примет вид:
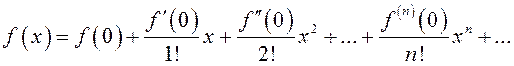 . (13.16)
. (13.16)
Степенной ряд (13.16) называется рядом Маклорена.
Остаточный член в форме Лагранжа (13.15) в этом случае имеет вид:
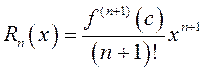 , (13.17)
, (13.17)
где ![]() находится между
находится между ![]() и
и
![]() .
.
Как было доказано
выше, ряд (13.16) сходится к функции ![]() для
всех
для
всех ![]() , при которых
, при которых ![]() .
.
ЛЕММА. 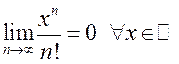 . (13.18)
. (13.18)
ДОКАЗАТЕЛЬСТВО. Рассмотрим степенной ряд (13.12) с общим членом 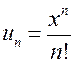 . В п.13.2.2 было показано, что он
сходится на всей числовой прямой, откуда по необходимому признаку сходимости
следует, что
. В п.13.2.2 было показано, что он
сходится на всей числовой прямой, откуда по необходимому признаку сходимости
следует, что 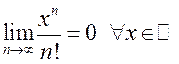 .
.
Что и требовалось доказать.
Представим основные элементарные функции в виде ряда Маклорена (13.16).
1.
![]() .
.
Вычислим
коэффициенты ряда 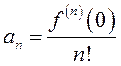 .
.
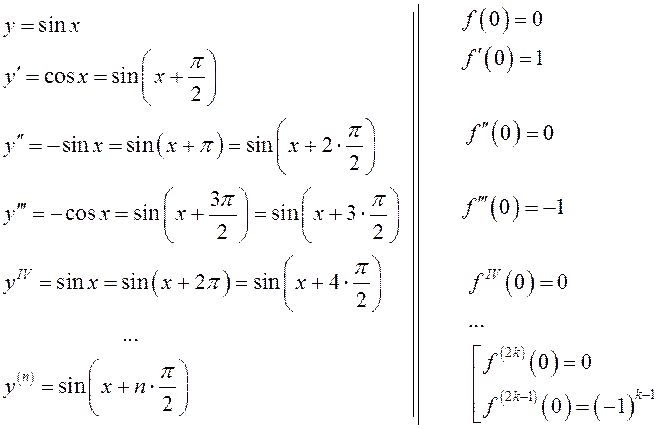
Составим формальный ряд:
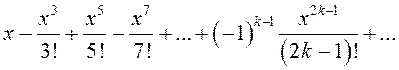 . (13.19)
. (13.19)
Его остаточный член (13.17) имеет вид:
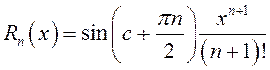 . Так как
. Так как  , то с
учетом (13.18) получаем, что
, то с
учетом (13.18) получаем, что ![]()
![]() , а это означает, что ряд (13.19) сходится
на всей числовой оси к функции, для которой он составлен.
, а это означает, что ряд (13.19) сходится
на всей числовой оси к функции, для которой он составлен.
Таким образом,
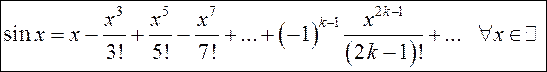 . (13.20)
. (13.20)
ПРИМЕР.
Вычислить приближенно  с точностью
с точностью ![]() .
.
Как известно,
функция 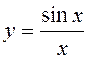 не имеет элементарной первообразной (см.
гл.7), поэтому нельзя найти точное значение этого интеграла с помощью формулы
Ньютона-Лейбница.
не имеет элементарной первообразной (см.
гл.7), поэтому нельзя найти точное значение этого интеграла с помощью формулы
Ньютона-Лейбница.
Для приближенного вычисления воспользуемся разложением (13.20) и теоремой об оценке остатка знакочередующегося ряда:
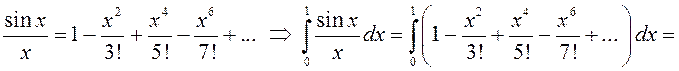
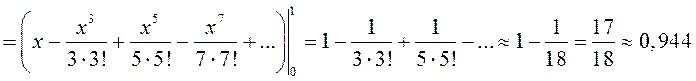
с точностью ![]() .
.
2. ![]() .
.
Степенной
ряд (13.20) можно почленно дифференцировать, при этом его интервал сходимости
не изменится. Поэтому, вычислив производную от обеих частей (13.20), получим
разложение в ряд Маклорена функции ![]() :
:
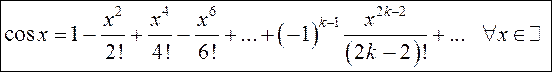 . (13.21)
. (13.21)
3. ![]() .
.
Так как ![]() , то
, то ![]() , и
формальный ряд для этой функции имеет вид:
, и
формальный ряд для этой функции имеет вид:
 .
.
Его
остаточный член в форме Лагранжа 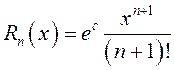 , где
, где ![]() находится между
находится между ![]() и
и
![]() . Исследуем поведение остаточного члена
ряда.
. Исследуем поведение остаточного члена
ряда.
Если ![]() , то
, то 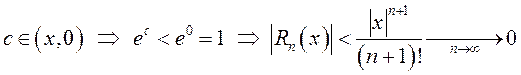 .
Значит,
.
Значит, ![]() при всех
при всех ![]() .
.
Если ![]() , то
, то 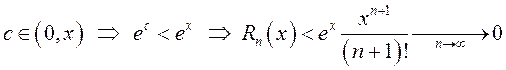 при любом
фиксированном
при любом
фиксированном ![]() . Следовательно, и при всех
. Следовательно, и при всех ![]()
![]() .
.
Таким образом,
составленный формальный ряд сходится на всей числовой оси к функции ![]() . Поэтому
. Поэтому
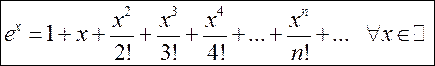 . (13.22)
. (13.22)
Из (13.22), в частности, следует, что
 .
.
4. 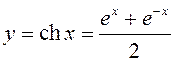 – гиперболический косинус
– гиперболический косинус ![]() .
.
Заменив
в (13.22) ![]() на
на ![]() ,
получим:
,
получим:
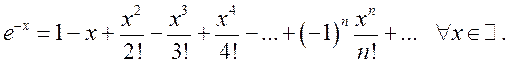 (13.23)
(13.23)
Найдем теперь полусумму абсолютно сходящихся рядов (13.22) и (13.23):
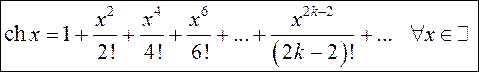 .
.
5. 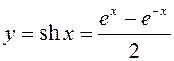 – гиперболический синус
– гиперболический синус ![]() .
.
Разложение в ряд этой функции может быть получено как полуразность рядов (13.22) и (13.23):
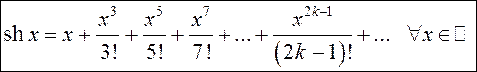 .
.
6. ![]() .
.
Заметим,
что 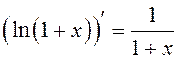 , а выражение
, а выражение 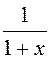 можно
трактовать как сумму бесконечно убывающей геометрической прогрессии, у которой
в соответствии с (13.1) первый член
можно
трактовать как сумму бесконечно убывающей геометрической прогрессии, у которой
в соответствии с (13.1) первый член ![]() , а знаменатель
, а знаменатель ![]() , причем
, причем ![]() . Следовательно,
. Следовательно,
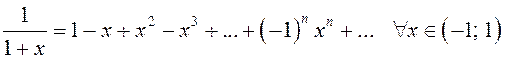 .
.
Так как  , то, проинтегрировав этот ряд почленно на
интервале сходимости, получим:
, то, проинтегрировав этот ряд почленно на
интервале сходимости, получим:
 . (13.24)
. (13.24)
ЗАМЕЧАНИЕ. Ряд (13.24) сходится не только во всех точках интервала
![]() , то и при
, то и при ![]() , что
легко проверяется с помощью признака Лейбница. Поэтому можно заключить, что
, что
легко проверяется с помощью признака Лейбница. Поэтому можно заключить, что
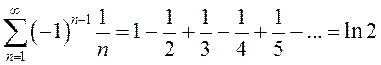 .
.
7. ![]() .
.
Вычислим
коэффициенты ряда  .
.
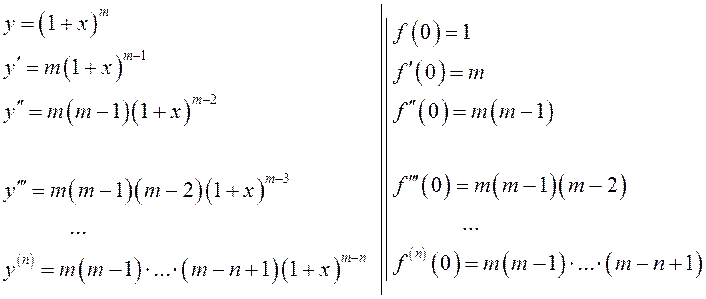
Составим формальный ряд:
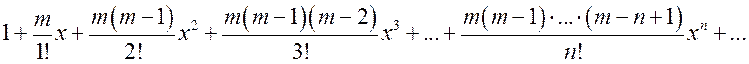 .
.
Поведение при ![]() остаточного члена этого ряда
остаточного члена этого ряда
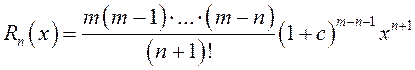 (13.25)
(13.25)
весьма трудоемко. Поэтому найдем его интервал сходимости: составим ряд из модулей членов ряда и применим признак Даламбера.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.