Числовые и функциональные ряды: Конспект лекций (Геометрическая прогрессия. Экстремальное свойство сумм Фурье), страница 6

        ТЕОРЕМА (признак Лейбница). Если для знакочередующегося ряда 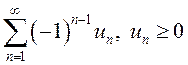 выполнены условия:

1.  ,

2.  , то ряд сходится и его сумма .

        ДОКАЗАТЕЛЬСТВО.  По определению ряд сходится, если существует конечный предел последовательности его частичных сумм: .

 

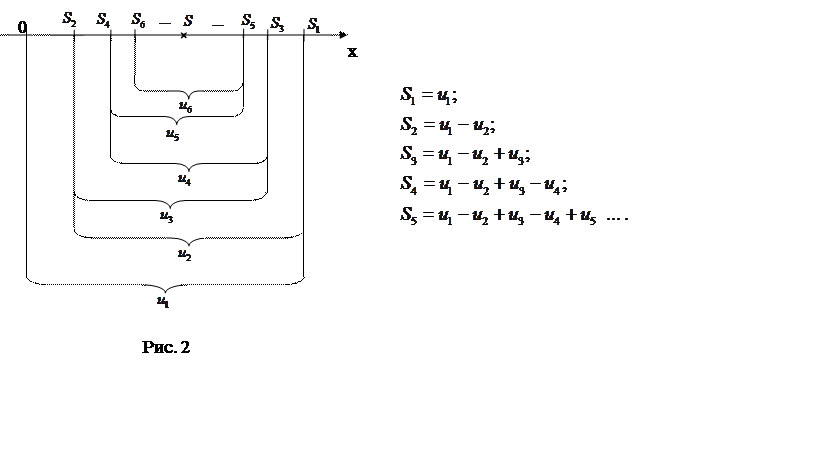По условию  теоремы , поэтому  (рис.2), кроме того, из рисунка ясно, что . Таким образом, последовательность частичных сумм  с четными номерами  возрастает  и ограничена сверху, значит, она имеет конечный предел (см. гл.4): .

По той же причине  (рис.2), но , то есть                 последовательность частичных сумм с нечетными номерами  возрастает  и ограничена снизу, значит, и она имеет конечный предел (см. гл.4): .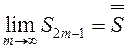

Но , откуда , так как по второму условию теоремы  . Значит, . Следовательно, существует конечный  () и потому ряд сходится.

Рис. 2 иллюстрирует тот факт, что сумма ряда .

Что и требовалось доказать.

        ПРИМЕР. Исследовать на сходимость ряд  .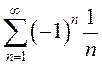

Для этого ряда 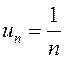 и потому оба условия признака Лейбница выполнены: ;  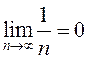. Значит, данный знакочередующийся ряд сходится. 

Заметим, что ряд, составленный их модулей членов этого ряда, является гармоническим  , то есть расходящимся.

Возвращаясь к предыдущему примеру, можно сделать вывод, что сходящиеся  знакопеременные ряды бывают двух типов: для одних ряд, составленный из модулей их членов, сходится, а  для других – расходится.

        ОПРЕДЕЛЕНИЕ. Знакопеременный ряд называется условно сходящимся, если он сходится, а ряд, составленный из модулей его членов, расходится.

        ОПРЕДЕЛЕНИЕ. Знакопеременный ряд называется абсолютно сходящимся, если сходится  ряд, составленный из модулей его членов.

Таким образом, можно заключить, что 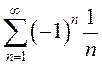   сходится условно, а

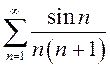 – абсолютно.  Нетрудно доказать, что  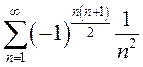– также  абсолютно сходящийся ряд.

Абсолютно сходящиеся ряды обладают свойствами конечных сумм, что утверждает следующая теорема.

        ТЕОРЕМА. Если знакопеременный ряд сходится абсолютно, то он остается абсолютно сходящимся  и при любой перестановке его членов, при этом сумма ряда от перестановки не зависит.

Без доказательства.

Условно сходящиеся ряды свойствами конечных сумм не обладают.

        ТЕОРЕМА. Если знакопеременный ряд сходится условно, то каково бы     ни было число А, можно подобрать такую бесконечную перестановку его членов, в результате которой сумма полученного ряда будет равна А. Более того, существуют перестановки, делающие условно сходящийся ряд расходящимся.

Без доказательства.

        ПРИМЕР. Как было показано выше, знакочередующийся ряд 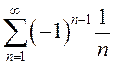  сходится условно. Приведем пример бесконечной перестановки его членов, в результате которой сумма возрастет в 1,5 раза.

Обозначим сумму этого ряда :

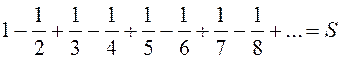                     .                                (13.6)

Умножим обе части (13.6) на :

              .                           (13.7)

Перепишем (13.7) таким образом:

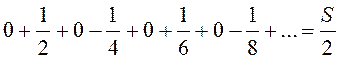                     .                              (13.8)

Складывая теперь (13.6) и (13.8), получим:

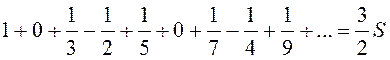, то есть                            

         .

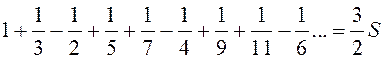С одной стороны данный ряд представляет собой сумму рядов (13.6) и (13.7),                 и потому его сумма равна 1,5. С другой стороны, как нетрудно увидеть, этот ряд получен бесконечной перестановкой членов исходного условно сходящегося ряда (13.6), именно: при такой перестановке после двух положительных                 членов ряда берется один отрицательный.

Таким образом, сделанная перестановка изменила сумму ряда.

13.1.6. ОСТАТОК  РЯДА  И  ЕГО  ОЦЕНКА

Если ряд сходится, то существует конечный  . Точное значение суммы  ряда, как правило, найти непросто, но из определения предела последовательности следует, что  при достаточно больших . А это значит, что сумму ряда  можно приблизить его частичной суммой  с любой наперед заданной точностью, взяв в частичной сумме достаточное число членов ряда.

Напомним, что  называется  -м остатком сходящегося ряда и   . Отсюда следует, что остаток  может быть сколь угодно мал при достаточно больших . Поэтому задача приближенного отыскания суммы ряда с заданной точностью  сводится к поиску такого номера , чтобы .