Числовые и функциональные ряды: Конспект лекций (Геометрическая прогрессия. Экстремальное свойство сумм Фурье), страница 5

а) 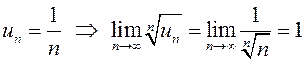, значит, радикальным признаком Коши так же, как и признаком Даламбера, при исследовании гармонического ряда пользоваться нельзя. Он, как известно, расходится.

б) 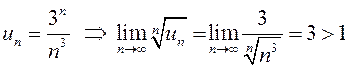, значит, данный ряд расходится.                      Заметим, что ранее этот ряд был исследован с помощью признака Даламбера и, как  здесь, так и там .

в)  – радикальный признак Коши                  не подходит для исследования данного ряда. Однако заметим, что .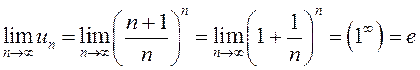

Так как  , то ряд расходится по необходимому признаку.

г) 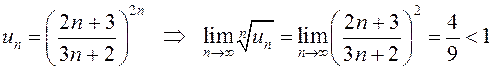, значит, ряд сходится по радикальному признаку Коши.

        ТЕОРЕМА (интегральный признак Коши). Пусть 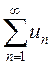 – знакоположительный ряд, члены которого не возрастают, то есть . Кроме               того, существует непрерывная невозрастающая функция  такая, что . Тогда, если

1)  несобственный интеграл 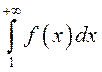  сходится, то ряд  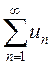 тоже                          сходится;

2)  несобственный интеграл 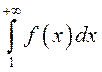  расходится, то ряд  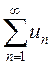 тоже                        расходится.

        ДОКАЗАТЕЛЬСТВО. Зафиксируем произвольное значение                         и построим график функции  ,  .

 

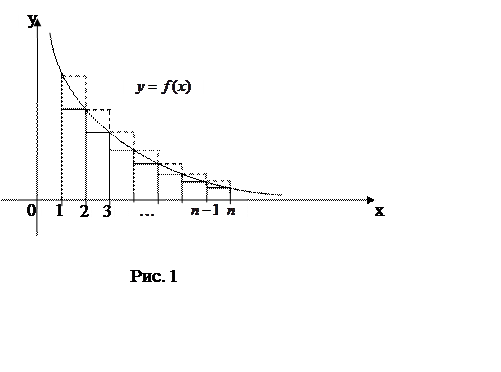Рассмотрим две ступенчатые фигуры: вписанную  в криволинейную трапецию, ограниченную построенным графиком, осью  и прямыми  и ,                     и описанную  вокруг нее (рис.1). Очевидно, что их площади удовлетворяют следующему неравенству (см. п.8.2):

Так как по условию , то это неравенство можно переписать                                                      таким образом:

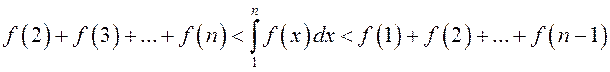, или  

                           .                                       (13.5)

1)  Пусть несобственный интеграл 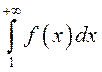  сходится. По определению                 несобственного интеграла с бесконечным верхним пределом интегрирования (см. п.8.7) существует конечный 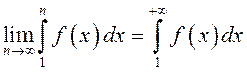 . Кроме того, так как по условию , то 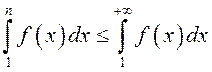.  Тогда из неравенства (13.5) имеем: 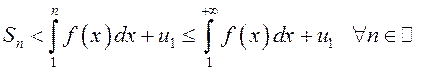. Это означает, что  ограничена сверху, то есть 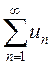 сходится.

2)  Пусть несобственный интеграл 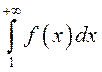  расходится. Так как по условию функция  монотонна, то 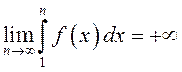. Из (13.5) имеем: 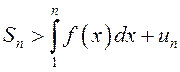. Отсюда 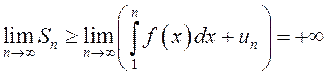 , то есть по определению  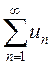 расходится.

Что и требовалось доказать.

        ПРИМЕР. Исследовать на сходимость ряд Дирихле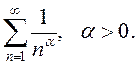

Применим интегральный признак Коши: рассмотрим функцию 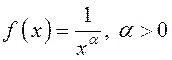.  Нетрудно  проверить, что  она  удовлетворяет  условиям  теоремы. Как известно (см. п.8.7), 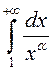 сходится при  и расходится при . Поэтому ряд Дирихле 

 

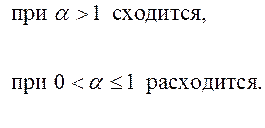
13.1.5.  ЗНАКОПЕРЕМЕННЫЕ    РЯДЫ

        Знакопеременными называются числовые ряды, имеющие члены разных знаков.

        ПРИМЕРЫ.

а) 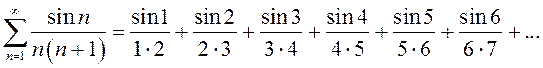. Так как значения  для углов в первой и второй четвертях положительны, то первые три                       члена этого ряда также положительны; 4, 5, 6 радиан – углы, принадлежащие промежутку , поэтому следующие три члена отрицательны и т.д.;

б)  ;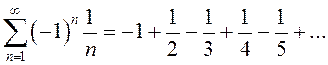

в)   .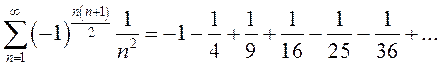

Если знаки членов ряда чередуются через один, то такой знакопеременный ряд называют знакочередующимся, то есть знакочередующийся ряд – частный случай знакопеременного.

В рассмотренном выше примере ряд б) – знакочередующийся.

        ТЕОРЕМА (достаточный признак сходимости знакопеременного ряда).   Если для знакопеременного ряда 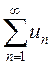 сходится ряд 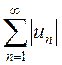, составленный                      из модулей его членов, то данный знакопеременный ряд сходится.

        ДОКАЗАТЕЛЬСТВО. Рассмотрим числовой ряд 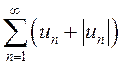. Легко                    убедиться, что , поэтому он является знакоположительным.

По условию 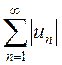 сходится, отсюда  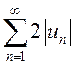также сходится, поэтому ряд 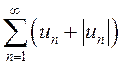 сходится по первому признаку сравнения.

Но 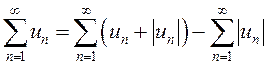, откуда данный знакопеременный ряд сходится как разность сходящихся рядов (свойство 1 числовых рядов).

Что и требовалось доказать.

        ПРИМЕР. Исследовать на сходимость .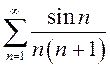

Рассмотрим ряд, составленный из модулей членов этого ряда: 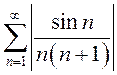.   Так как  то . Ранее было доказано, что знакоположительный ряд 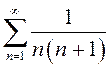  сходится. Следовательно, данный знакопеременный ряд сходится.

        ЗАМЕЧАНИЕ. Доказанный достаточный признак не является необходимым признаком сходимости знакопеременного ряда, поэтому из расходимости ряда 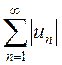 нельзя сделать вывод о поведении знакопеременного ряда .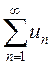

Докажем теперь более простой в применении признак сходимости знакочередующихся рядов. Заметим, что знакочередующиеся ряды – частный случай рядов знакопеременных, поэтому доказанный выше признак может быть тоже использован для исследования поведения таких рядов.