Что и требовалось доказать.
ПРИМЕР.
Исследовать на сходимость ряд 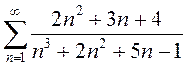 .
.
Обозначим 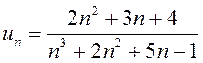 . Поведение числителя и знаменателя этой дроби
определяется их старшими степенями, поэтому ряд для сравнения выберем так:
. Поведение числителя и знаменателя этой дроби
определяется их старшими степенями, поэтому ряд для сравнения выберем так: 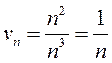 ,
, 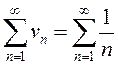 –
гармонический ряд.
–
гармонический ряд.
Найдем 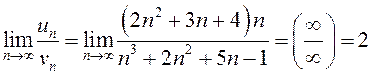 (см.гл.4). Этот предел конечен и отличен
от нуля, значит, оба ряда ведут себя одинаково, то есть расходятся по
предельному признаку сравнения.
(см.гл.4). Этот предел конечен и отличен
от нуля, значит, оба ряда ведут себя одинаково, то есть расходятся по
предельному признаку сравнения.
ТЕОРЕМА
(признак Даламбера). Пусть  –
знакоположительный ряд и существует
–
знакоположительный ряд и существует 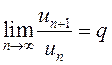 . Если
. Если
![]() , то ряд сходится; если
, то ряд сходится; если ![]() – ряд расходится.
– ряд расходится.
ДОКАЗАТЕЛЬСТВО.
По условию 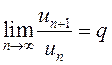 . По определению предела последовательности
(см.гл.4)
. По определению предела последовательности
(см.гл.4)
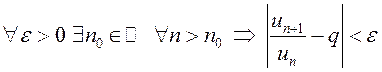 , или
, или
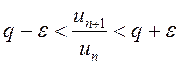 . (13.3)
. (13.3)
1) Пусть ![]() . Выберем
. Выберем ![]() так,
что
так,
что ![]() . Тогда из (13.3) имеем:
. Тогда из (13.3) имеем: ![]() . В частности,
. В частности,
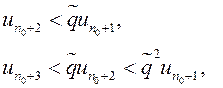
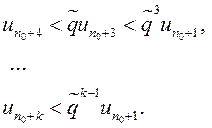
Обозначим ![]() . Это общий член геометрической прогрессии
со знаменателем
. Это общий член геометрической прогрессии
со знаменателем ![]() и первым членом
и первым членом ![]() . Такая прогрессия сходится, поэтому ряд
. Такая прогрессия сходится, поэтому ряд
 сходится по первому признаку сравнения и
свойству 2 числовых рядов (п.13.1.2).
сходится по первому признаку сравнения и
свойству 2 числовых рядов (п.13.1.2).
2) Пусть
![]() . Выберем
. Выберем ![]() так,
что
так,
что ![]() . Тогда из (13.3) имеем:
. Тогда из (13.3) имеем: ![]() .
. 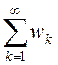 – ряд
геометрической прогрессии, знаменатель которой
– ряд
геометрической прогрессии, знаменатель которой ![]() . Такая
прогрессия расходится, поэтому ряд
. Такая
прогрессия расходится, поэтому ряд  расходится по второму
признаку сравнения и свойству 2 числовых рядов.
расходится по второму
признаку сравнения и свойству 2 числовых рядов.
ЗАМЕЧАНИЕ. Из доказательства следует, что если 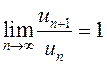 ,
то есть
,
то есть ![]() , то с помощью этого признака
исследовать поведение ряда
, то с помощью этого признака
исследовать поведение ряда  нельзя. Если
нельзя. Если ![]() , то ряд может, как сходиться, так и расходиться,
а признак Даламбера для его исследования – неподходящий
инструмент. Поэтому в таких случаях надо применять другие признаки сходимости.
, то ряд может, как сходиться, так и расходиться,
а признак Даламбера для его исследования – неподходящий
инструмент. Поэтому в таких случаях надо применять другие признаки сходимости.
ПРИМЕРЫ. С помощью признака Даламбера исследовать сходимость
рядов: а)
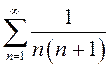 ; б)
; б) ![]() ; в)
; в) 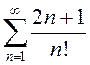 ; г)
; г) 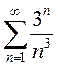 .
.
а) 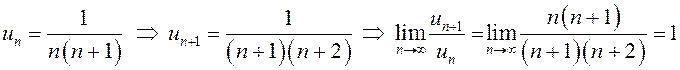 .
.
Это
означает, что признак Даламбера для исследования сходимости такого ряда не
подходит. Ранее было показано, что 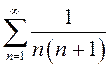 сходится.
сходится.
б) 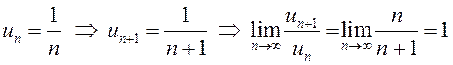 , следовательно, и в данном случае
признаком Даламбера пользоваться нельзя. Но
, следовательно, и в данном случае
признаком Даламбера пользоваться нельзя. Но ![]() – гармонический
ряд, который, как было доказано, расходится.
– гармонический
ряд, который, как было доказано, расходится.
в) Общий член этого ряда содержит функцию натурального аргумента, которая называется «эн факториал».
По определению ![]() – произведение всех целых чисел от
1 до
– произведение всех целых чисел от
1 до ![]() . Тогда
. Тогда ![]() .
.
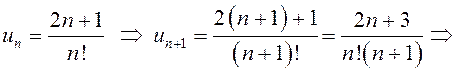
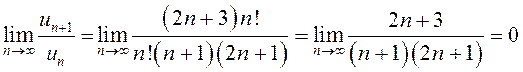 , так как степень
числителя меньше степени знаменателя (см. гл.4).
, так как степень
числителя меньше степени знаменателя (см. гл.4).
Таким
образом, ![]() , значит, данный ряд сходится по признаку
Даламбера.
, значит, данный ряд сходится по признаку
Даламбера.
г) 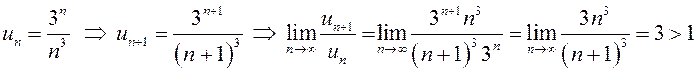 ,
,
значит, данный ряд расходится по признаку Даламбера.
ЗАМЕЧАНИЕ. Из рассмотренных примеров следует, что с помощью признака Даламбера можно исследовать ряды, общий член которых содержит показательную функцию или (и) факториал.
ТЕОРЕМА
(радикальный признак Коши). Пусть  –
знакоположительный ряд и существует
–
знакоположительный ряд и существует ![]() .
Если
.
Если ![]() , то ряд сходится;
, то ряд сходится;
если ![]() – ряд расходится.
– ряд расходится.
ДОКАЗАТЕЛЬСТВО.
По условию ![]() . По определению предела последовательности
(см.гл.4)
. По определению предела последовательности
(см.гл.4) ![]() , или
, или
![]() . (13.4)
. (13.4)
1) Пусть
![]() . Выберем
. Выберем ![]() так,
что
так,
что ![]() . Тогда из (13.4) имеем:
. Тогда из (13.4) имеем: ![]() . Обозначим
. Обозначим ![]() .
. 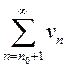 – ряд геометрической прогрессии со
знаменателем
– ряд геометрической прогрессии со
знаменателем ![]() , поэтому
, поэтому 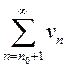 сходится,
значит,
сходится,
значит,  сходится по первому
признаку сравнения и свойству 2 числовых рядов.
сходится по первому
признаку сравнения и свойству 2 числовых рядов.
2)
Пусть ![]() . Выберем
. Выберем ![]() так,
что
так,
что ![]() . Тогда из (13.4) имеем:
. Тогда из (13.4) имеем: ![]() .
. ![]() – общий
член геометрической прогрессии, знаменатель которой
– общий
член геометрической прогрессии, знаменатель которой ![]() .
Такая прогрессия расходится, поэтому ряд
.
Такая прогрессия расходится, поэтому ряд
 расходится по второму признаку сравнения и
свойству 2 числовых рядов.
расходится по второму признаку сравнения и
свойству 2 числовых рядов.
ЗАМЕЧАНИЕ.
Из доказательств радикального признака Коши и признака Даламбера следует, что с
их помощью можно исследовать поведение тех рядов, общий член которых сравним с
общим членом геометрической прогрессии. Если это не так, то применение и того,
и другого признака не приведет к определенному результату (получим ![]() ). Поэтому если
). Поэтому если ![]() ,
то для исследования ряда надо выбрать другой признак, но не
признак Даламбера.
,
то для исследования ряда надо выбрать другой признак, но не
признак Даламбера.
ПРИМЕРЫ.
С помощью радикального признака Коши исследовать сходимость
рядов: а) ![]() ; б)
; б) 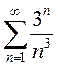 ; в)
; в) 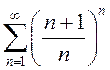 ; г)
; г) 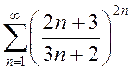 .
.
При использовании радикального признака Коши полезно вспомнить, что
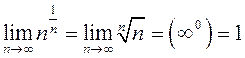 , а также что
, а также что
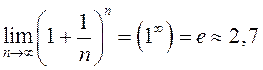
(второй замечательный предел) (см. гл.4).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.