Таким образом,
область сходимости этого ряда – интервал ![]() . Сумма
ряда определена
. Сумма
ряда определена ![]() и находится по формуле (13.1):
и находится по формуле (13.1): 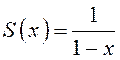 .
.
Итак, 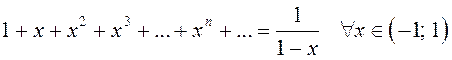 . С другой стороны, можно сказать, что во
всех точках интервала
. С другой стороны, можно сказать, что во
всех точках интервала ![]() функция
функция 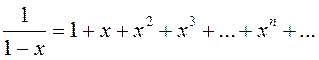 ,
то есть разлагается в ряд, членами которого являются степенные
функции, и поэтому он называется степенным.
,
то есть разлагается в ряд, членами которого являются степенные
функции, и поэтому он называется степенным.
13.2.2. СТЕПЕННЫЕ РЯДЫ
ОПРЕДЕЛЕНИЕ. Функциональный ряд вида
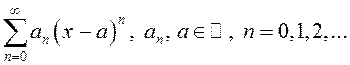 (13.9)
(13.9)
называется степенным
рядом по степеням разности ![]() .
.
Если в
(13.9) положить ![]() , то получим степенной ряд по
степеням
, то получим степенной ряд по
степеням ![]() :
:
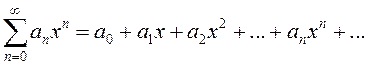 (13.10)
(13.10)
Область
сходимости ряда (13.9), очевидно, зависит от коэффициентов ряда, но содержит, по
крайней мере, одну точку ![]() , то есть является непустой.
, то есть является непустой.
Найдем,
при каких значениях ![]() ряд (13.10) сходится.
ряд (13.10) сходится.
При
каждом фиксированном значении ![]() (13.10) – числовой и,
вообще говоря, знакопеременный ряд. Применим к нему
достаточный признак сходимости знакопеременных рядов (см.п.13.1.5): рассмотрим
ряд
(13.10) – числовой и,
вообще говоря, знакопеременный ряд. Применим к нему
достаточный признак сходимости знакопеременных рядов (см.п.13.1.5): рассмотрим
ряд 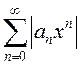 , составленный из модулей членов ряда
(13.10).
, составленный из модулей членов ряда
(13.10).
Поведение этого знакоположительного ряда исследуем по признаку Даламбера (см.п.13.1.4): найдем
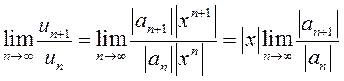 . (13.11)
. (13.11)
Полагая, что 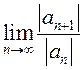 существует, конечен и не равен нулю,
обозначим
существует, конечен и не равен нулю,
обозначим 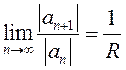 . Тогда, возвращаясь к (13.11), получим:
. Тогда, возвращаясь к (13.11), получим: 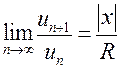 .
.
Отсюда ряд
(13.10) сходится абсолютно, если 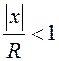 , или
, или ![]() .
.
Если 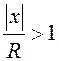 , или
, или ![]() , то
ряд из модулей расходится, при этом общий член исходного ряда (13.10) не
стремится к нулю, и потому ряд расходится по необходимому признаку сходимости.
, то
ряд из модулей расходится, при этом общий член исходного ряда (13.10) не
стремится к нулю, и потому ряд расходится по необходимому признаку сходимости.
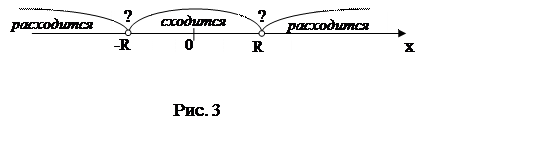
Если же ![]() , то признак Даламбера не подходит для
исследования поведения ряда (13.10) (рис.3).
, то признак Даламбера не подходит для
исследования поведения ряда (13.10) (рис.3).
 |
ОПРЕДЕЛЕНИЕ.
Число ![]() , определяемое равенством
, определяемое равенством 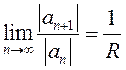 , называется радиусом сходимости
степенного ряда (13.10). Интервал
, называется радиусом сходимости
степенного ряда (13.10). Интервал ![]() называется интервалом
сходимости этого ряда.
называется интервалом
сходимости этого ряда.
ОПРЕДЕЛЕНИЕ.
Областью сходимости степенного ряда (13.10) называется его интервал
сходимости, к которому, быть может, присоединены точки ![]() и
(или)
и
(или) ![]() .
.
ЗАМЕЧАНИЕ.
Если 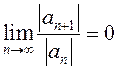 , то полагают, что
, то полагают, что ![]() и
степенной ряд (13.10) сходится на всей числовой прямой.
и
степенной ряд (13.10) сходится на всей числовой прямой.
Если же 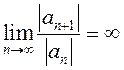 , то считается, что
, то считается, что ![]() и
область сходимости ряда (13.10) состоит из одной точки
и
область сходимости ряда (13.10) состоит из одной точки ![]() .
.
ПРИМЕР. Найти область сходимости степенного ряда
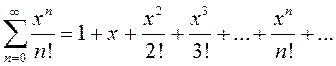 . (13.12)
. (13.12)
(По определению
считается, что ![]() ).
).
Применим к ряду,
составленному из модулей членов данного, признак Даламбера: 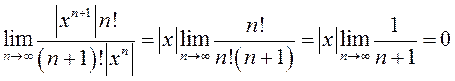 при любом фиксированном
при любом фиксированном ![]() . Следовательно, ряд (13.12) абсолютно
сходится на всей числовой прямой.
. Следовательно, ряд (13.12) абсолютно
сходится на всей числовой прямой.
Для того
чтобы найти интервал сходимости степенного ряда (13.9), обозначим
![]() . Тогда ряд
. Тогда ряд 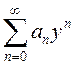 абсолютно
сходится при
абсолютно
сходится при ![]() , где
, где ![]() его
радиус сходимости. Отсюда интервал сходимости ряда (13.9) определяется неравенством
его
радиус сходимости. Отсюда интервал сходимости ряда (13.9) определяется неравенством
![]() , или
, или ![]() .
.
ПРИМЕР.
Найти область сходимости степенного ряда 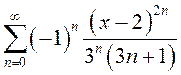 .
.
Составим ряд из
модулей 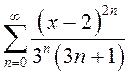 . Его общий член
. Его общий член
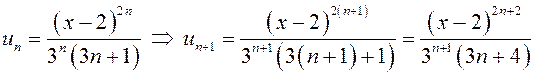 .
.
По признаку Даламбера этот ряд сходится, если
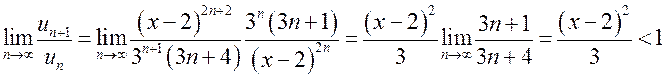 .
.
Решим это неравенство:
![]() .
.
Следовательно,
при всех ![]() ряд сходится абсолютно.
ряд сходится абсолютно.
Исследуем
поведение ряда в крайних точках его интервала сходимости ![]() .
.
При ![]() исходный степенной ряд становится
знакочередующимся числовым рядом:
исходный степенной ряд становится
знакочередующимся числовым рядом:
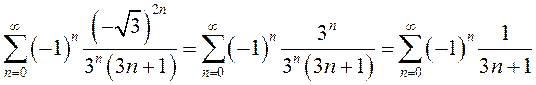 .
.
Легко проверить,
что этот ряд сходится по признаку Лейбница (см.п.13.1.5), то есть точка ![]() принадлежит области сходимости.
принадлежит области сходимости.
Аналогично при ![]() получим числовой ряд
получим числовой ряд
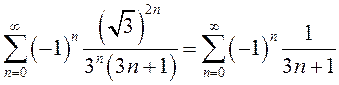 .
.
Он совпадает с
предыдущим, поэтому точка ![]() также принадлежит области
сходимости исходного ряда.
также принадлежит области
сходимости исходного ряда.
Итак, ![]() .
.
13.2.3. СВОЙСТВА СТЕПЕННЫХ РЯДОВ
Рассмотрим степенной ряд по
степеням ![]() (13.10), который сходится на интервале
(13.10), который сходится на интервале ![]() .
.
Ряд вида
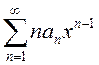 называется степенным рядом, полученным
из (13.10) почленным дифференцированием.
называется степенным рядом, полученным
из (13.10) почленным дифференцированием.
Ряд вида
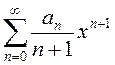 называется степенным рядом, полученным
из (13.10) почленным интегрированием.
называется степенным рядом, полученным
из (13.10) почленным интегрированием.
ТЕОРЕМА 1. Почленное дифференцирование или интегрирование степенного ряда не изменяют его интервала сходимости.
ДОКАЗАТЕЛЬСТВО.
Пусть степенной ряд 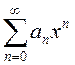 сходится
сходится ![]() .
Радиус сходимости
.
Радиус сходимости ![]() по определению находится из
равенства
по определению находится из
равенства 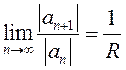 .
.
Рассмотрим ряд 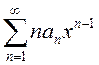 . Найдем его интервал сходимости, применив признак
Даламбера к знакоположительному ряду
. Найдем его интервал сходимости, применив признак
Даламбера к знакоположительному ряду 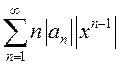 :
:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.