Числовые и функциональные ряды: Конспект лекций (Геометрическая прогрессия. Экстремальное свойство сумм Фурье), страница 14

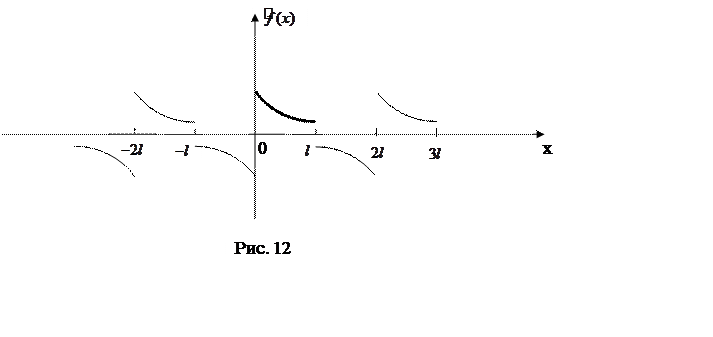
Если продолжить  нечетным образом на отрезок  (рис.12),                   то разложение в ряд Фурье функции  будет содержать только синусы.                    Поэтому можно сказать, что в этом случае  разложена на отрезке                      в ряд по синусам.

 

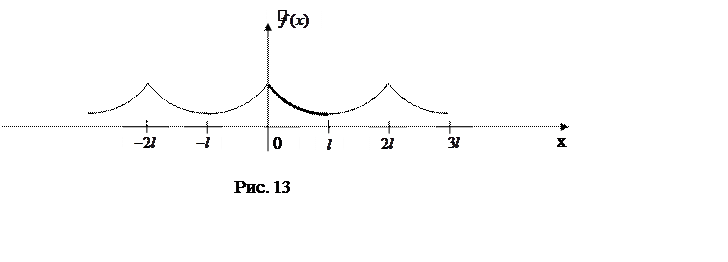
Если построить четное продолжение функции  на промежуток  (рис.13), то ряд Фурье такой функции будет содержать только косинусы. В этом случае будем говорить, что  разложена на отрезке  в ряд по косинусам.

Не следует думать, что  для одной и той же функции можно таким образом получить два различных разложения в ряд Фурье.  На самом деле  в ряд разлагались две весьма отличающиеся функции (рис.12 и 13), совпадающие лишь при , и суммы полученных таким образом рядов совпадают только для . Использование значений этих сумм за пределами отрезка  постановка такой задачи не предполагает.

ПРИМЕР. Разложить функцию  в ряд: а) по синусам;    б) по косинусам.

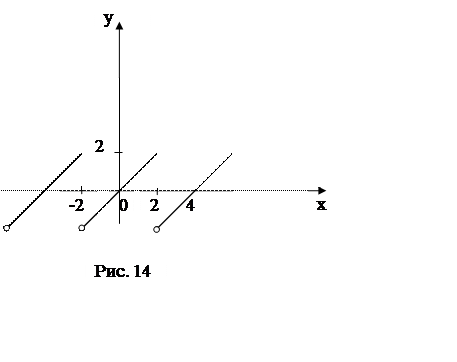
а) Построим нечетное периодическое продолжение данной функции                      с периодом  (рис.14).

 

Тогда по формуле (13.41)   

. 

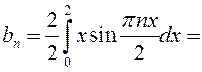
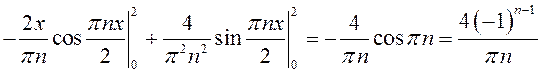Отсюда

.

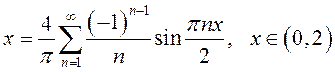Заметим, что сумма полученного ряда в соответствии с теоремой Дирихле равна нулю и при , и при  (рис.14).

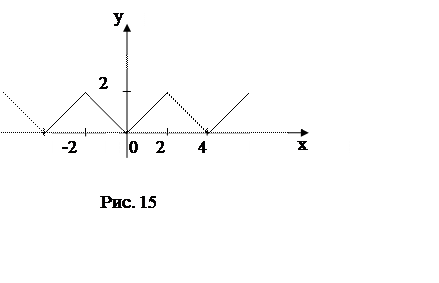
б) Построим четное периодическое продолжение данной функции  с периодом  (рис.15).

 

Тогда по формулам (13.40)

.

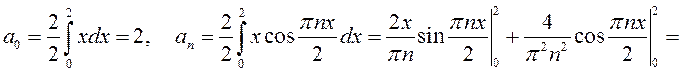
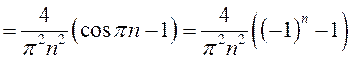В этом случае имеем:

.

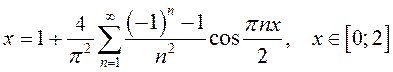Заметим, что четное периодическое продолжение заданной функции непрерывно (рис.15), поэтому .

13.2.10. ЭКСТРЕМАЛЬНОЕ  СВОЙСТВО  СУММ  ФУРЬЕ

Представление периодических функций в виде ряда Фурье имеет на практике тот смысл, что , где -я частичная сумма ряда.                 Точность этого приближенного равенства в соответствии с определением                   суммы ряда можно сделать сколь угодно высокой выбором достаточно большого .

Функция вида

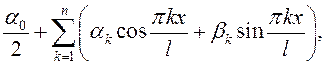                                                      (13.42)

  называется тригонометрическим многочленом -го порядка.

Выясним, какой характер имеет приближенное представление                                    -периодической функции  тригонометрическими многочленами вида (13.42).

В данном случае за меру погрешности естественно взять среднее квадратичное отклонение

.

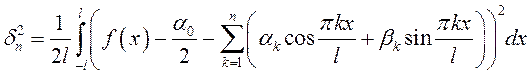Поставим следующую задачу: пусть -периодическая функция  удовлетворяет условиям Дирихле на отрезке ; среди всех тригонометрических многочленов -го порядка найти путем выбора коэффициентов  тот многочлен, для которого величина  имеет минимальное значение.

Чтобы решить эту задачу, рассмотрим  как функцию переменных  и найдем ее частные производные первого порядка                      по этим переменным. По необходимому условию экстремума функции                                            нескольких переменных (см.гл.6) эти производные в точке минимума равны нулю:

.  

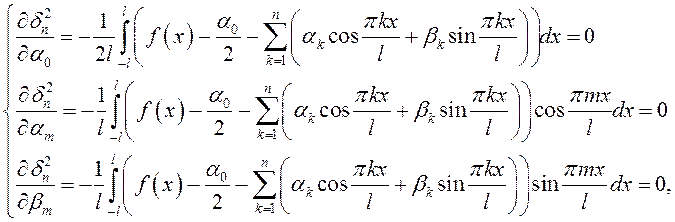
Так как 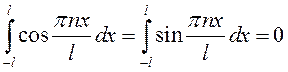, то из первого уравнения этой системы получим: 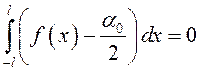 . Отсюда .

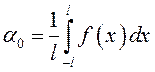Далее, так как

,

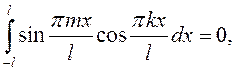
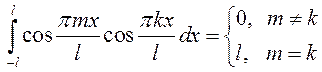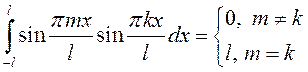 (см.п. 13.2.6), то  из второго и третьего уравнений системы имеем:

.

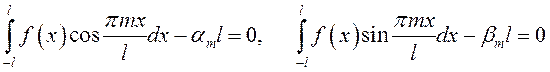Тогда         

.

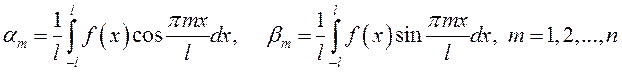Таким образом, числа  являются соответствующими                      коэффициентами Фурье функции .

Проверка достаточного условия экстремума показывает, что при найденных значениях коэффициентов функция  достигает именно минимума,                        однако ее можно и не делать, так как способ задания  вполне очевидно показывает, что такая функция  имеет экстремум, причем именно минимум.

Это означает, что суммы Фурье наилучшим образом описывают в целом  поведение -периодической функции.

       Библиографический список

1.  Воробьев, Н.Н. Теория рядов./ Н.Н. Воробьев.– М.: Лань, 2002.– 416 с.

2.  Пискунов, Н.С. Дифференциальное и интегральное исчисления. Т.2. /     Н.С. Пискунов.– М.: Интеграл–пресс, 2009.– 544 c.

3.  Фихтенгольц, Г.М. Основы математического анализа./ Г.М. Фихтенгольц.– М.: Лань, 2005.– 464 с.

Редактор

Компьютерная верстка, дизайн обложки

ИД № 06039 от 12.10.2001 г.

Сводный темплан 2012 г.

Подписано в печать     .  .  . Формат 60×84  ¹/₁₆. Бумага офсетная.

Отпечатано на дупликаторе. Усл. печ. л.      . Уч.-изд. л.          .

Тираж      . Заказ  .

______________________________________________________

Издательство ОмГТУ. 644050, г. Омск, пр-т Мира, 11

Типография ОмГТУ