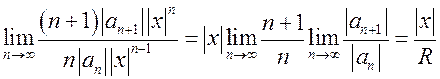Числовые и функциональные ряды: Конспект лекций (Геометрическая прогрессия. Экстремальное свойство сумм Фурье), страница 9

, так как  (см.гл.4).

Следовательно, ряд сходится, если 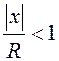, то есть .

Утверждение теоремы для ряда, полученного из (13.10) почленным интегрированием, доказывается аналогично.

        ЗАМЕЧАНИЕ. Несмотря на неизменность интервала сходимости степенного ряда при почленном дифференцировании или интегрировании, область сходимости при выполнении этих действий может измениться.

        ТЕОРЕМА 2. Сумма степенного ряда (13.10) является непрерывной функцией, определенной на интервале сходимости.

Без доказательства.

ТЕОРЕМА 3. Во всех точках интервала сходимости степенной ряд можно почленно дифференцировать, при этом  .

Без доказательства.

ТЕОРЕМА 4. Во всех точках интервала сходимости степенной  ряд можно почленно интегрировать, при этом

.

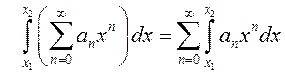Без доказательства.

ЗАМЕЧАНИЕ.  Две последние теоремы представляют собой аналог хорошо известных фактов: производная суммы равна сумме производных и интеграл от суммы равен сумме интегралов. Однако доказательство этих теорем для степенных рядов гораздо сложнее их конечных аналогов и потому выходит за рамки данного курса.

Рассмотрим пример применения сформулированных свойств.

ПРИМЕР.  Найти сумму  степенного ряда

.

Обратим внимание на то, что после почленного дифференцирования этот ряд станет рядом геометрической прогрессии со знаменателем :

.

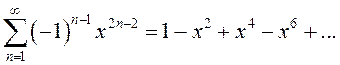Ряд сходится, если , то есть . По свойству 1 интервалы сходимости обоих рядов совпадают, а по свойству 3 и формуле (13.1) 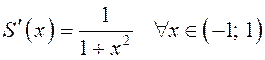. Отсюда .

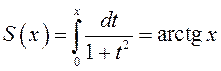Таким образом, получено разложение функции  в степенной ряд по степеням  :

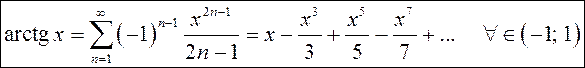   .        (13.13)

Этим разложением можно пользоваться для приближенных вычислений.

ПРИМЕР. Вычислить 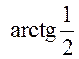 и  приближенно с точностью .

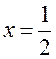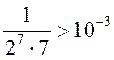Подставив  в (13.13), имеем:. Так как , а 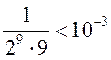, то по теореме об оценке остатка ряда, сходящегося по признаку Лейбница (см.п.13.1.6.),

 

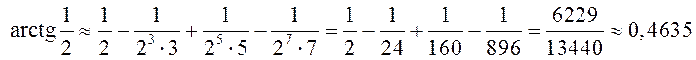
с точностью .

Ряд (13.13) при  расходится, поэтому вычислить приближенно  по аналогии нельзя.  В этом случае следует воспользоваться известным тождеством 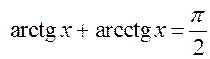 и тем, что 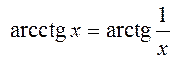. Таким образом, зная значение 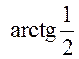, получаем

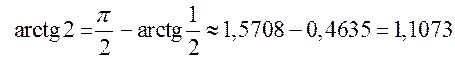 с точностью .

        ЗАМЕЧАНИЕ.  Заметим, что область сходимости ряда (13.13) отличается от области сходимости ряда, полученного из него почленным дифференцированием, именно, нетрудно проверить, что  (13.13) сходится .

13.2.4.  РАЗЛОЖЕНИЕ  ФУНКЦИИ  В  СТЕПЕННОЙ РЯД.

РЯД   ТЕЙЛОРА

Пусть  функция  является суммой степенного ряда:

              (13.14) или, по-другому,  разложена в степенной ряд (13.14).

Найдем, каким образом коэффициенты этого ряда связаны с .

При  имеем:  .

Чтобы найти коэффициент , продифференцируем (13.14) на интервале сходимости:

.

Тогда при  получим:  .

Вычислив вторую производную

и полагая , имеем: .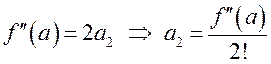

Действуя далее аналогично, получим, что ,…, или   .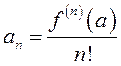

Таким образом, если функцию  можно разложить в степенной ряд по степеням разности , то разложение имеет вид:

.

Этот степенной ряд называется рядом Тейлора для функции  в окрестности точки  .

Последнее равенство было получено формально, поэтому теперь необходимо ответить на два вопроса:

1.  Каким условиям должна удовлетворять функция  , чтобы для нее можно было составить ряд Тейлора?

2.  При каких  ряд Тейлора сходится,  причем именно к той функции, для которой он составлен?                                                                                                       

Ответ на первый вопрос очевиден: если функция имеет производную любого порядка, то есть является бесконечно дифференцируемой в окрестности точки , то коэффициенты ее ряда Тейлора могут быть найдены по формуле , .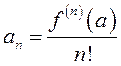

Чтобы ответить на второй вопрос, представим функцию в виде

, где 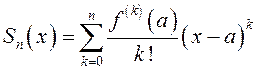 – -я частичная сумма,                      а    назовем остаточным членом ряда Тейлора.

ТЕОРЕМА (необходимое и достаточное условие сходимости ряда          Тейлора). Для того чтобы ряд Тейлора, составленный для бесконечно дифференцируемой в окрестности точки  функции , сходился к , необходимо и достаточно, чтобы  .

ДОКАЗАТЕЛЬСТВО.

1.  Необходимость: сумма ряда .

По определению суммы ряда

.

2.  Достаточность:  .

. Отсюда ,                     то есть по определению ряд сходится и его сумма .

Что и требовалось доказать.

Таким образом,  будет суммой составленного для нее ряда Тейлора для всех , при которых .