Учебное пособие по решению контрольных задач, страница 9

Находим горизонтальные проекции точек 3 и N (в нашем примере N¢ была построена ранее):

3¢ Î L¢T¢,   N¢ Î x.

При проецировании на плоскость p₂ точка 3 «закрывает» точку N, следовательно, на фронтальной плоскости проекций отрезок KT также видимый, а отрезок KL – невидимый.

7.2. Плоскость задана плоской фигурой (рис.7.5)

1. Через прямую LT проводим вспомогательную горизонтально-проецирующую плоскость b (рис.7.6):

 º L¢T¢,    ^ x.

2. Строим линию пересечения EF заданной и вспомогательной плоскостей (рис.7.7):

E¢ = A¢В¢ Ç ;

E² находится в пересечении линии проекционной связи, проведенной из Е¢, и A²B²;

F¢ = А¢C¢ Ç ;

F² находится в пересечении линии проекционной связи, проведенной из Е¢, и A²C².

3. Строим точку пересечения K заданной прямой LT и линии пересечения EF:

K² = L²T² Ç E²F²;

K¢ находится в пересечении линии проекционной связи, проведенной из K², и L¢T¢.

4. Определяем взаимную видимость прямой LT и треугольника АВС с помощью конкурирующих точек (рис.7.8). На горизонтальной плоскости проекций выбираем конкурирующие точки в пересечении L¢T¢ с любой из проекций прямых, принадлежащих плоскости треугольника АВС, например 1¢ º Е¢ = = L¢T¢ Ç A¢B¢:

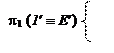1 Î LT;

E Î AB.

В направлении на плоскость p₁ точка E² «закрывает» точку 1², следовательно, на горизонтальной плоскости проекций отрезок 1K закрыт от непосредственного обзора треугольником ABC.

На фронтальной плоскости проекций выбираем конкурирующие точки в пересечении L²T² с любой из проекций прямых, принадлежащих плоскости треугольника АВС, например 2² º 3² = L²T² Ç A²B²:

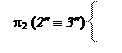2 Î LT;

3 Î АВ.

В направлении на плоскость p₂ точка 3¢ «закрывает» точку 2¢, следовательно, на фронтальной плоскости проекций отрезок 2K невидимый.

Задача 8

Построить линию пересечения двух заданных плоскостей. Показать взаимную видимость плоскостей.

8.1. Одна плоскость задана следами, другая – плоской фигурой (рис.8.1)

1. Линия пересечения двух плоскостей, как уже говорилось выше, определяется двумя точками, общими для этих плоскостей. В данном случае две такие точки могут быть найдены, как точки пересечения любых сторон плоской фигуры с плоскостью a.

2. Находим точку пересечения K₁ прямой АС с плоскостью a (см. задачу 7): через прямую АC проводим вспомогательную плоскость, например фронтально-проецирую­щую плоскость b (рис.8.2), находим линию пересечения М₁N₁ плоскостей a и b и в ее пересечении с прямой АС определяем искомую точку K₁ с проекциями  и .

3. Находим точку пересечения K₂ прямой BС с плоскостью a: проводим вторую вспомогательную плоскость, например горизонтально-проецирую­щую плоскость g (рис.8.3), находим линию пересечения М₂N₂ плоскостей a и g и в ее пересечении с прямой BС определяем искомую точку K₂ с проекциями  и .

4. Зная точки K₁ и K₂, общие для плоскости a и плоскости треугольника ABC, проводим через них линию пересечения K₁K₂ с проекциями  и  (рис.8.4).

5. Определяем видимость плоскостей друг относительно друга на основе анализа положения конкурирующих точек, например: точек 1 и М₂ – на горизонтальной плоскости проекций и точек 2 и N₁ – на фронтальной плоскости проекций (см. задачу 7).

8.2. Обе плоскости заданы плоскими фигурами (рис.8.5)

1. В данном случае две точки, общие для плоскостей, заданных плоскими фигурами, могут быть найдены двумя способами:

· как точки пересечения сторон одной фигуры с плоскостью второй фигуры;