Учебное пособие по решению контрольных задач, страница 8

 

Задача 6

Построить линию пересечения плоскостей a и b. Показать видимость линии пересечения.

Индивидуальное задание приведено на рис.6.1.

1. Линию пересечения плоскостей проводят через две любые общие для этих плоскостей точки. Если плоскости заданы следами, то такими точками будут точки пересечения одноименных следов. В данном случае одну точку (точку М), общую для заданных плоскостей (рис.6.2), находим в пересечении горизонтальных следов этих плоскостей:

М¢ =  Ç ;  M² Î x.

2. Поскольку фронтальные следы заданных плоскостей в пределах чертежа не пересекаются, для построения второй точки, общей для заданных плоскостей, проводим вспомогательную плоскость (рис.6.3), например горизонтальную плоскость g ( || x). Находим горизонтальные проекции линий пересечения плоскости g с плоскостями a и b. Горизонтальная проекция линии пересечения плоскостей g и a проходит через  параллельно , а горизонтальная проекция линии пересечения плоскостей g и b – через  параллельно .

3. В пересечении горизонтальных проекций линий пересечения вспомогательной и заданных плоскостей находим проекцию K¢ (рис.6.4). Из K¢ проводим линию проекционной связи до пересечения с  и отмечаем проекцию K². Точка K (K¢, K²) – общая для заданных плоскостей a и b.

4. Через одноименные проекции двух точек, общих для плоскостей a и b, проводим проекции линии пересечения, горизонтальную М¢K¢ и фронтальную М²K². Обозначаем видимость линии пересечения: она считается видимой на том участке, который находится в I октанте.

Задача 7

Построить точку пересечения прямой LT с заданной плоскостью. Показать видимость прямой относительно заданной плоскости.

7.1. Плоскость задана следами (рис.7.1)

1. Для построения точки пересечения прямой LT с плоскостью a проводим через прямую вспомогательную плоскость, например фронтально-проецирующую плоскость b (рис.7.2):

 º L²T²;   ^ x.

2. Строим линию пересечения МN заданной и вспомогательной плоскостей (рис.7.3):

М¢ =  Ç ;  М² º Х_b;

N² =  Ç ;  N¢ Î x.

На чертеже проекция М² не показана, так как в дальнейших построениях она не используется.

3. Определяем точку пересечения K заданной прямой LT с линией пересечения МN:

K¢ = L¢T¢ Ç М¢N¢;

K² находится в пересечении линии проекционной связи, проведенной из K¢, с фронтальной проекцией L²T².

4. Определяем взаимную видимость прямой LT и плоскости a, которая считается непрозрачной (рис.7.4). Взаимная видимость определяется раздельно при проецировании на плоскости p₁ и p₂.

Выбираем конкурирующие точки для определения видимости в направлении на горизонтальную плоскость проекций. В пересечении L¢T¢ и  совмещаются проекции точек 1 и 2, из которых одна принадлежит прямой LT, а другая – плоскости a. Пусть

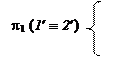1 Î LT;

2 Î .

Находим фронтальные проекции точек 1 и 2:

1² Î L²T², 2² Î x.

При проецировании на плоскость p₁ точка 1 «закрывает» точку 2. Следовательно, точка 1, лежащая на прямой LT, находится ближе к наблюдателю, чем точка 2. Таким образом, отрезок KТ расположен над плоскостью a, обозначаем его линией видимого контура. Отрезок KL находится под плоскостью a и на горизонтальной плоскости проекций считается невидимым.

Выбираем конкурирующие точки для определения взаимной видимости в направлении на плоскость p₂. В пересечении L²T² и  совмещаются фронтальные проекции двух точек, из которых одна принадлежит прямой LT, а другая – плоскости a:

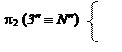3 Î LT;

N Î