7. Аналогично строим грани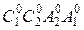 
и 
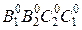. К полученной развертке боковой
поверхности достраиваем основания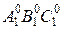 
и 
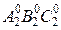. Построенная фигура является разверткой
полной поверхности заданной призмы.
8. Находим на развертке положение точек K1
и K2.
Для этого через точку K1
проводим вспомогательную прямую ED, а через точку K2
– прямую FG, параллельные ребрам (см. рис.20.8). Затем
находим положение этих вспомогательных прямых и точек K1
и K2
на плоскости p4
и на развертке.
20.3. Конус
(рис.20.10)
1. При помощи двух
пересекающихся прямых задаем вспомогательную плоскость a, проходящую через заданную прямую и вершину конуса. Одна из прямых LT,
а другая – прямая, проходящая через вершину конуса S и любую точку
прямой LT, например точку Т (рис.20.11).
2. Строим проекции горизонтальных следов прямой LT
(
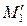) и вспомогательной прямой ST (
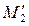). Через эти точки проводим горизонтальный
след вспомогательной плоскости a –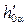 
.
3. След 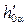пересекает
основание конуса, лежащее в плоскости проекций p1,
в точках 1 и 2. Сечение конуса плоскостью a представляет собой треугольник S12 (рис.20.12).
4. Искомые точки
пересечения прямой LT с поверхностью конуса (K1 и K2)
находим в пересечении прямой с контурами сечения (рис.20.13).
5. Определяем
видимость прямой относительно поверхности конуса: в направлении на p1
невидимым будет отрезок, ограниченный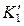 
и
образующей конуса, а в направлении на p2 – отрезок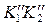 
.
6. Строим развертку поверхности конуса. В заданный
конус вписываем шестиугольную пирамиду (рис.20.14),
основанием которой является правильный шестиугольник 134567.
7. Способом вращения вокруг оси i,
перпендикулярной плоскости p1
и проходящей через вершину S, определяем натуральную величину ребер
пирамиды. В плоскости p1
горизонтальные проекции ребер пирамиды вращаются вокруг точки i¢ до положения, параллельного оси х. Тогда на фронтальной плоскости
проекций мы получим их натуральные величины (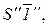
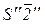и т.д.).
Основание конуса лежит в горизонтальной плоскости проекций,
и, следовательно, проецируется на эту плоскость в натуральную величину.
8. В свободном месте
чертежа строим развертку поверхности пирамиды методом треугольников (рис.20.15) по известной длине их сторон (см. задачу
20.1). Через построенные на развертке вершины пирамиды 60, 50,
40 … проведем по лекалу плавную кривую линию, концы
которой соединяем отрезками с вершиной S0.
9. К
построенной развертке боковой поверхности конуса пристраиваем основание – окружность,
радиус которой равен радиусу горизонтальной проекции основания (эта окружность
вычерчивается в любом месте чертежа без наложения на развертку боковой
поверхности, но так, чтобы с построенной кривой линией – развернутым контуром
основания – она имела одну общую точку).
10. Наносим
положение точек пересечения K1 и K2 на развертку. Для этого первоначально проводим
через них образующие (образующая S1, на которой лежит K1,
уже имеется) и определяем
натуральную величину расстояний от
вершины конуса
S до точек
K1и
K2 – это отрезки
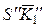
и
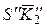
(см. рис. 20.13 и 20.14).
