Учебное пособие по решению контрольных задач, страница 10

· одна точка как точка пересечения стороны первой фигуры с плоскостью второй фигуры, а другая – как точка пересечения стороны второй фигуры с плоскостью первой фигуры.

2. Находим точку K₁ () пересечения стороны AC треугольника АВС с плоскостью треугольника EDF (рис.8.6):

· через прямую АС проводим вспомогательную плоскость, например фронтально-проецирующую плоскость a;

· строим линию пересечения 12 плоскости a и треугольника EDF;

· определяем горизонтальную проекцию точки встречи

 = А¢С¢ Ç 1¢2¢

и ее фронтальную проекцию

 Î А²С².

3. Аналогично находим точку K₂ (,) пересечения другой стороны треугольника АВС, например стороны BC с плоскостью треугольника EDF (рис.8.7). Для этого через сторону ВС проводим вспомогательную горизонтально-проеци­рующую плоскость b, строим линию пересечения 34 плоскостей b и треугольника EDF и определяем проекции точки встречи K₂:

 = B²C² Ç 3²4²;

 Î В¢С¢.

4. Зная две точки, общие для заданных плоскостей DАВС и DEDF, проводим через них линию пересечения K₁K₂ ( и ) (рис.8.8).

5. Определяем видимость плоских фигур друг относительно друга при помощи анализа положения конкурирующих точек.

Выбираем конкурирующие точки для определения видимости на горизонтальной плоскости проекций, например в пересечении горизонтальных проекций В¢С¢ и D¢F¢:

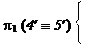4 Î (DF);

5 Î (BC).

По фронтальной проекции точек 4 и 5 видно, что точка 4 находится выше точки 5, поэтому на горизонтальной плоскости проекций прямая DF будет закрывать прямую ВС. Следовательно, в этой части треугольник EDF будет ближе к наблюдателю, чем треугольник АВС, и участок треугольника АВС, ограниченный прямой DF и линией пересечения K₁K₂, будет невидимым. От противного по другую сторону линии пересечения ближе к наблюдателю окажется треугольник АВС, который закроет часть стороны EF треугольника EDF.

Выбираем конкурирующие точки для определения видимости на фронтальной плоскости проекций, например в пересечении фронтальных проекций А²С² и Е²D²:

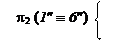1 Î (ED);

6 Î (AC).

Рассматривая горизонтальные проекции точек 1 и 6, видим, что точка 1 находится ближе к наблюдателю. Следовательно, в направлении на плоскость p₂ прямая ED закрывает прямую АС, и в этой области треугольник ЕDF будет ближе к наблюдателю, чем треугольник АВС. Поэтому на фронтальной плоскости проекций часть треугольника АВС, ограниченная прямой ED и линией пересечения K₁K₂, будет невидимой. Рассуждая от противного, по другую сторону от линии пересечения ближе к наблюдателю окажется треугольник АВС, закрывающий от обзора часть стороны EF треугольника EDF.

Задача 9

Определить истинную величину расстояния от точки K до заданной плоскости.

9.1. Плоскость задана следами (рис.9.1)

1. Опускаем перпендикуляр из точки K на заданную плоскость (рис.9.2): фронтальная проекция перпендикуляра проводится из точки K² перпендикулярно фронтальному следу плоскости , а горизонтальная проекция перпендикуляра – из точки K¢ перпендикулярно горизонтальному следу плоскости .

2. Строим точку пересечения перпендикуляра с плоскостью a (см. задачу 7), для чего через перпендикуляр проводим вспомогательную плоскость, например фронтально-проецирующую плоскость b (рис.9.3). Точка L (L¢, L²) – искомая точка пересечения.

3. Определяем истинную величину отрезка KL методом прямоугольного треугольника (см. задачу 2): строим прямоугольный треугольник по двум катетам (один катет – горизонтальная проекция отрезка K¢L¢, другой – алгебраическая разность координат Dz_KL = K¢K₀). Гипотенуза K₀L¢ – искомое расстояние (рис.9.4).

9.2. Плоскость задана плоской фигурой (рис.9.5)