Теория параллельных прямых. Теория треугольника, страница 9

4. Объясните полученный результат.

2.2.3. О признаках равенства треугольников.

В связи с тем, что определение равенства треугольников достаточно сложное для проверки, возникает необходимость в признаках равенства, то есть в возможности определить равенство треугольников по меньшему количеству элементов. Но простым перебором можно получить только признак равенства по трем сторонам. Остальные признаки можно получить, заменив равенство сторон равенством противолежащих углов.

2.2.4. Задачи на построение треугольников по трем элементам не включены в текст учебника, но их необходимо рассматривать на уроках, для лучшего усвоения признаков равенства треугольников.

Глава 3. Теория параллельных прямых.

В начале изучения курса геометрии вы познакомились с разными случаями взаимного расположения геометрических фигур на плоскости. Нерассмотренным остался случай отношения прямых. Начнем с изучения взаимного расположения двух прямых.

3.1. Взаимное расположение двух прямых.

В каком отношении могут находиться две прямые?

Две прямые на плоскости могут иметь одну общую точку (рис.3.1). В этом случае прямые принято называть пересекающимися.

Пересекающиеся прямые – это общий случай взаимного расположения прямых на плоскости. В этом случае ещё говорят, что прямые находятся в общем положении.

Возможны ли другие случаи взаимного расположения двух прямых?

Да, и мы можем сделать два предположения: 1. Две прямые на плоскости не могут иметь больше одной общей точки; 2. Две прямые на плоскости могут не иметь общих точек.

Предлагаем эти предположения обсудить во время групповой дискуссии.

Для простоты дальнейших изложений примем две аксиомы.

А₁. Две точки однозначно определяют прямую.

То есть мы не будем различать совпадающие прямые.

А₂. Существуют прямые на плоскости, которые не имеют общих точек.

Две прямые на плоскости, не имеющие общих точек, принято называть непересекающимися (рис.3.2).

Непересекающиеся прямые – это особый случай взаимного расположения прямых на плоскости.

Рис.3.1

Рис.3.2

Как вы думаете, сколько можно провести прямых, пересекающихся с данной прямой, и не пересекающихся с данной прямой?

Вопрос. А сколько можно провести прямых через одну точку так, чтобы они пересекались с данной прямой? Сколько прямых, непересекающихся с данной, можно провести через точку, не лежащую на этой прямой?

Рассмотрим произвольную прямую a и точку M, не лежащую на ней (рис.3.5). Через точку M проведём произвольную прямую. Сколько таких прямых можно провести? Таких прямых существует бесконечно много.

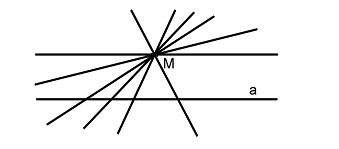
Рис.3.3

Мы видим, что среди этих прямых много прямых, пересекающихся с прямой а. А сколько  прямых,  непересекающихся с  прямой а проходит через  точку М? Возможные ответы: одна, ни одной, несколько. На рис.3.3 видно, что, по крайней мере, одна такая прямая существует. Но сколько таких прямых – мы сказать не можем.

Но действительно ли нужно отвечать на этот вопрос?

Рассмотрим два случая такого взаиморасположения трех прямых, при котором без ответа на этот вопрос возникает противоречие.

1) Прямые а и b не пересекаются. Прямая c пересекает прямую a. Пересекает ли прямая c прямую b (рис.3.4)? Может и не пересечь, если через одну точку можно провести больше одной прямой, непересекающейся с данной. Но на рисунке видно, что прямые с и b пересекутся.