|
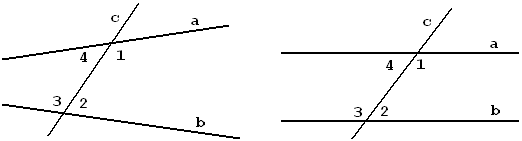
Рис.3.20 |
Рис.3.21 |
Эти углы принято называть внутренними односторонними, так как они расположены внутри параллельных прямых и в одной полуплоскости относительно секущей.
Раз одни и те же углы составляют пары и внутренних односторонних и внутренних накрест лежащих углов, то между ними должна быть связь. Посмотрите внимательнее на рисунки 3.20 и 3.21.
Пара внутренних накрест лежащих углов, например 2 и 4, и пара внутренних односторонних углов, например 1 и 2, имеют один общий угол – 2,а углы 1 и 4 – смежные, то есть Ð1+Ð4=180º. Значит, если углы 2 и 4 равны, то сумма углов 1 и 2 равна 180º, и наоборот. Поэтому верно утверждение
Если внутренние накрест лежащие углы равны, то сумма внутренних односторонних углов равна 180°. И обратно: если сумма внутренних односторонних углов равна 180°, то внутренние накрест лежащие углы равны.
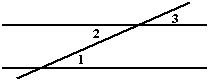 Если у пары внутренних накрест лежащих углов один угол
заменить вертикальным ему, то получится пара углов, которые называются соответственными
углами данных прямых с секущей. На рисунке справа углы 1 и 3– соответственные.
Если у пары внутренних накрест лежащих углов один угол
заменить вертикальным ему, то получится пара углов, которые называются соответственными
углами данных прямых с секущей. На рисунке справа углы 1 и 3– соответственные.
Из равенства внутренних накрест лежащих углов следует равенство соответственных и наоборот (Докажите это утверждение самостоятельно).
Объединим три утверждения, связывающие различные виды углов в одно.
Утверждение 3.1. Внутренние накрест лежащие углы равны, сумма внутренних односторонних углов равна 180°, соответственные углы равны - это три эквивалентных высказывания. То есть справедливость одного из них влечет справедливость остальных двух.
Раз верно утверждение 3.1, то мы можем сформулировать еще два признака параллельности прямых.
Теорема 3.3(II признак параллельности двух прямых). Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Задание 3. Сформулируйте и докажите обратное утверждение.
Теорема 3.4(III признак параллельности двух прямых). Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.
Задание 4. Как формулируется и доказывается обратное утверждение?
Обобщая вышеизложенное, можно сказать, что параллельность двух прямых можно определить по углам, которые эти прямые образуют с третьей прямой, пересекающей их (секущей).
Утверждение 3.2. Прямые параллельны, соответственные углы равны, внутренние накрест лежащие углы равны, сумма внутренних односторонних углов равна 180° - это четыре эквивалентных высказывания. То есть справедливость одного из них влечет справедливость остальных двух.
Это утверждение следует из теорем 3.1, 3.2 и утверждения 1.
С помощью теорем, которые являются признаками параллельности двух прямых, можно доказать, что противоположные теоремы также верны.
I признак не параллельности прямых.
Если при пересечении двух прямых секущей внутренние накрест лежащие углы не равны, то прямые не параллельны.
Докажите это утверждение и сформулируйте обратное.
II признак не параллельности прямых.
Если при пересечении двух прямых секущей соответственные углы не равны, то прямые не параллельны.
Докажите эту теорему и сформулируйте обратную ей.
III признак не параллельности двух прямых.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.