Теория параллельных прямых. Теория треугольника, страница 19

Теорема 4.1. Сумма внутренних углов треугольника равна 180°.

Мы выяснили как ведут себя внутренние углы с той стороны, где прямые пересекаются. А что можно сказать об остальных углах. Три из них – вертикальные по отношению к внутренним углам треугольника, а остальные – смежные им углы. Для последних есть специальное название.

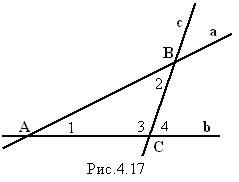Внешним углом треугольника при данной вершине принято называть угол, смежный с углом треугольника при этой вершине.

На рисунке 4.16 угол 4 – внешний угол треугольника АВС при вершине С.

По теореме о сумме углов треугольника Ð1+Ð2+Ð3=180°.

Отсюда следует, что

Ð1+Ð2=180°-Ð3=Ð4, то есть внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним. Мы доказала терему о внешних углах треугольника.

Теорема 4.2. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Из теоремы о сумме углов треугольника следует, что если в треугольнике один из углов прямой или тупой, то сумма двух других не превосходит 90º и, значит, каждый из них острый. Таким образом, в любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой

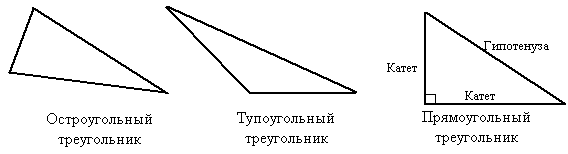
Рис.4.18

Если в треугольнике все три угла острые, то треугольник называется остроугольным. Если один из углов тупой, то треугольник называется тупоугольным. Если один из углов прямой, то треугольник называется прямоугольным. Сторона прямоугольного треугольника, лежащая против прямого угла называется гипотенузой, а две другие – катетами (рис.4.18).

4.2.2. Соотношение углов и сторон в треугольнике.

Посмотрите еще раз на треугольники, изображенные на рисунке 4.18. Видно, что в этих треугольниках против большей стороны лежит больший угол, а против большего угла лежит большая сторона. Попробуем доказать наше предположение.

Начнем с первой части: против большей стороны лежит больший угол.

Пусть в треугольнике АВС сторона АВ больше стороны АС (рис.4.19). Докажем, что ÐС>ÐВ.

Отложим на стороне АВ отрезок АЕ, равный стороне АС. Так как АЕ<АВ, то точка Е лежит между точками А и В. Следовательно, угол 1 является частью угла С и, значит, ÐС>Ð1. Угол 2 – внешний угол треугольника ВЕС, поэтому Ð2>ÐВ. Углы 1 и 2 равны, так как равны их соответствующие поперечины АЕ и АС. Таким образом, ÐС>Ð1, Ð1=Ð2, Ð2>ÐВ. Отсюда следует, что ÐС>ÐВ.

Посмотрите еще раз на рисунок 4.19. В треугольнике ЕАС равны две стороны ЕА и АС. Треугольники такого вида имеют специальное название.

Треугольник называется равнобедренным, если у него две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием треугольника. На рисунке справа DАВС – равнобедренный.

В равнобедренном треугольнике углы при основании равны (ÐВАС=ÐВСА), так как равны их соответственные поперечины (ВС=ВА).

Теперь докажем вторую часть предположения, обратную первой: против большего угла лежит большая сторона.

Пусть в треугольнике АВС ÐС>ÐВ. Докажем, что АВ>АС.

Предположим, что это не так. Тогда либо АВ=АС, либо АВ<АС. В первом случае треугольник АВС – равнобедренный, и, значит ÐС=ÐВ. Во втором случае ÐС>ÐВ (против большей стороны лежит больший угол). И то и другое противоречит условию ÐС>ÐВ. Поэтому наше предположение неверно, и, следовательно, АВ>АС. Итак, мы доказали наше предположение, а, значит, оно стало теоремой.