Сколько точек пересечения у прямой c с прямыми a иb в каждом из этих четырех случаев?
Прямую, которая пересекает две другие прямые, каждую в своей точке, принято называть их секущей.
Найдите секущие на рис.3.8 - 3.11.
Теперь попробуем ответить на поставленный выше вопрос 2: может ли прямая, пересекающая одну из двух параллельных прямых, не пересекать другую?
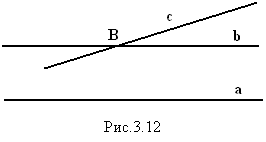 Пусть a и b - параллельные прямые, и пусть прямая с
пересекает прямую b в точке В
(рис.3.12).
Пусть a и b - параллельные прямые, и пусть прямая с
пересекает прямую b в точке В
(рис.3.12).
Если бы прямая c не пересекала прямую a, то через точку B проходили бы две прямые, параллельные прямой a: прямая b и прямая c. Но это противоречит аксиоме параллельности. Значит, прямая c, пересекая прямую b,должна пересекать и параллельную ей прямую a.
Итак, используя аксиому параллельности, мы доказали утверждение: если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую. Его принято называть следствием 1 из аксиомы параллельности.
Ответим теперь на вопрос 3:
Следствие 2 (из аксиомы параллельности). Если две прямые параллельны третьей прямой, то они параллельны между собой.
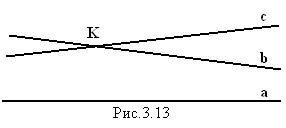 Предположим, что c и b не параллельны
(рис.3.13), значит, они пересекаются в какой-то точке K.
Тогда через точку K проведены две различные прямые,
параллельные прямой a, что противоречит аксиоме
параллельности. Поэтому c||b.
Что и требовалось доказать.
Предположим, что c и b не параллельны
(рис.3.13), значит, они пересекаются в какой-то точке K.
Тогда через точку K проведены две различные прямые,
параллельные прямой a, что противоречит аксиоме
параллельности. Поэтому c||b.
Что и требовалось доказать.
Итак, мы провели третью прямую, и с ее помощью уточнили представление о параллельных и пересекающихся прямых, и узнали, что две прямые параллельные третьей параллельны. Но как узнать, что каждая из этих двух прямых параллельна третьей? Можно ли сказать, что рассмотрение третьей прямой самой по себе не позволило нам ответить на вопрос 1? Да, поэтому теперь обратимся к исследованию углов, которые получаются при пересечении двух прямых третьей. Начнем с наблюдения.
Начертим две пересекающиеся прямые и две параллельные. Проведём к каждой паре прямых секущую (рис.3.14 и 3.15).
|
Рис.3.14 |
Рис.3.15 |
Вопрос 4. Сколько получится углов с вершиной в точках пересечения прямых и секущей? Что можно сказать о сравнительной величине этих углов?
Вы наверняка получили ряд точных утверждений о сравнительной величине каких-то пар углов, верных как пересекающихся так и для параллельных прямых, а так же получили, что сравнительная величина каких-то пар углов характерна только для параллельных прямых. Давайте последовательно рассмотрим эти характеристические пары.
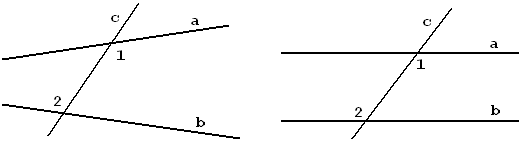
|
Рис.3.16, а |
Рис.3.17, а |
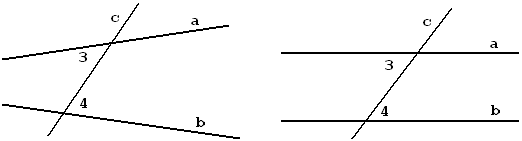
|
Рис.3.16, б |
Рис.3.17, б |
Посмотрите на рисунки 3.16 и 3.17. На них углы обозначены цифрами.
Сравним углы на рисунках слева и справа. На рисунках 3.16, а и б видно, что угол 1 больше угла 2, а угол 3 меньше угла 4. Эти углы принято называть внутренними накрест лежащими, так как они расположены внутри параллельных прямых и в разных полуплоскостях относительно секущей. Секущая c образует с прямыми a и b две пары внутренних накрест лежащих углов. Мы видим, что на рисунках 3.16, а и б внутренние накрест лежащие углы не равны.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.