Теория параллельных прямых. Теория треугольника, страница 15

Докажите это следствие самостоятельно.

Теперь возьмем случай трех параллельных прямых и их секущей. Рассмотрим частный случай такого расположения прямых, когда отрезки секущей, расположенные между параллельными прямыми равны (рис.3.28).

Но тогда расстояния между соседними параллельными прямыми равны, то есть параллельные прямые равноудалены. Здесь нам необходимо определение расстояния между параллельными прямыми. Определим сначала расстояние от точки до прямой.

За расстояние от точки до прямой можно взять длину перпендикуляра, опущенного из данной точки до прямой. Но вдруг такой перпендикуляр не один или его не всегда можно провести?

Теорема 3.5. Из любой точки, не лежащей на данной прямой, можно опустить на эту прямую перпендикуляр, и только один.

Доказательство. Пусть а – данная прямая и А – не лежащая на ней точка (рис.3.29). Проведем через какую-нибудь точку прямой а перпендикулярную ей прямую с. А теперь проведем через точку А параллельную ей прямую b. Она будет перпендикулярна прямой а, так как прямая а, будучи перпендикулярна одной из параллельных прямых, перпендикулярна и другой. Отрезок АВ прямой b и есть перпендикуляр, проведенный из точки А к прямой а.

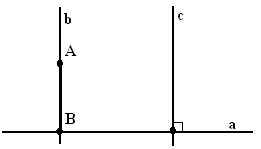
Рис.3.29

Единственность перпендикуляра АВ следует из принятой нами аксиомы о параллельности. Если бысуществовал другой перпендикуляр, проходящий через точку А, то через точку А проходило  бы две  прямые, параллельные  прямой с (так как две прямые перпендикулярные третьей параллельны). Теорема доказана.

Так как перпендикуляр, опущенный из данной точки до прямой, единственный и всегда существует, то его длину мы можем принять за расстояние от точки до прямой.

Длина перпендикуляра, опущенного из данной точки до прямой, называется расстоянием от точки до прямой.

Из леммы 1 и следствия 3 (из I признака параллельности прямых) получаем, что расстояния от всех точек прямой до прямой, параллельной ей, равны.

Расстоянием между параллельными прямыми называется расстояние от какой-нибудь точки одной прямой до другой прямой.

Так же верно обратное  утверждение:  равноотстоящие  прямые параллельны.

Прямые называются равноотстоящими, если каждая точка одной прямой равноудалена от другой прямой

Вернемся к случаю, когда отрезки секущей, расположенные между параллельными прямыми равны.

Лемма 2. Если отрезки секущей, расположенные между параллельными прямыми равны, то параллельные прямые равноудалены.

Доказательство. Нам дано, что AB=BC. (рис.3.30, а).

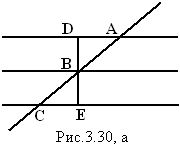Через точку В проведем прямую DE, перпендикулярную одной из трех параллельных прямых. Она будет перпендикулярна двум другим прямым (так как прямая, перпендикулярная одной из двух параллельных прямых перпендикулярна и другой).

Нам нужно доказать, что DB=BE.

УглыÐCBE и ÐABD равны как вертикальные. Углы ÐDAB и ÐECB равны как внутренние накрест лежащие при параллельных прямых AD иCE и секущейAC.

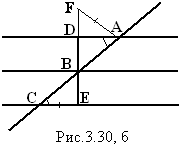На луче BD отложим отрезок BF, равный отрезку BE (рис.3.30, б). Углы ÐCBE и ÐABF равны, значит, их соответственные поперечины CE и AF равны (проверьте, действительно ли они являются соответственными). То есть BF и BE – соответственные поперечины углов ÐFAB и ÐECB, но они равны по построению, а значит, угол ÐFAB равен углу ÐECB. Но угол ÐECB равен углу ÐDAB. Это означает, что равны углы ÐFAB иÐDAB, то есть точка F лежит на луче AD. По построению точка F лежит на луче ВD. Но эти лучи пересекаются в точке D, то есть точки D и F совпадают и DB=BF=BE. Следовательно, DB=BE. Утверждение леммы 2 доказано.